1. 서 론

우주에서 임무를 수행하는 위성, 우주탐사선 등의 탑재체를 우주 공간으로 내보내기 위해서 지구의 중력을 이기는 에너지를 만들 수 있는 로켓을 사용한다. 로켓은 발사 후 1분 만에 음속을 돌파하며, 음속의 7배까지 속도를 올린다. 이런 극초음속 비행체는 이륙과 재진입 과정에서 공력가열이 일어난다[1,2,3,4,5]. 이로부터 탑재체를 보호하기 위하여 페어링을 사용한다. 페어링은 임무를 수행하기 위해 가장 중요한 탑재체를 보호하는 역할을 하기에 열보호 설계가 필수적이다. 하지만 열보호 설계가 필요 이상으로 과도할 경우 전체 발사 무게가 늘어나 발사 비용에 영향을 줄 수 있다. 그러므로 발사 후 지구를 벗어나는 동안 저항과 마찰열을 정확히 예측하고 적절한 열보호 설계를 하는 것이 중요하다.

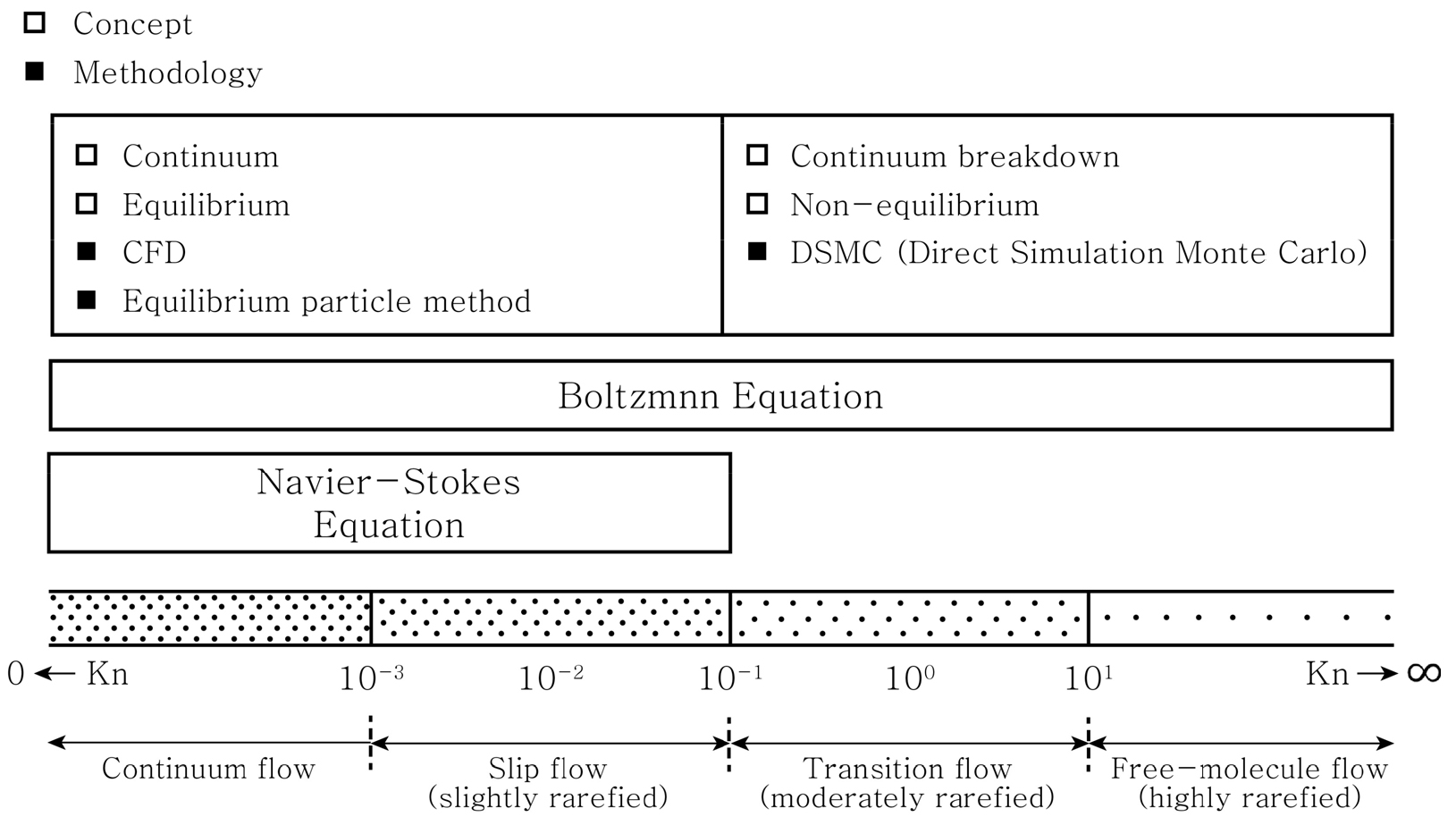
로켓이 지구 대기를 벗어나서 목표 궤도에 안착하기까지, 페어링은 저고도와 고고도 환경을 모두 경험한다. 저고도에서는 Navier-Stokes 방정식이 유효하며, 마하수가 높아서 충격파가 발생하며 압축성 유동 모델을 사용한 해석이 필요하다. 고고도 환경에서는 압력과 밀도가 지구 근처보다 매우 낮아 희박 유동의 특성을 가진다. 고고도에서는 몬테카를로 직접 모사법(Direct Simulation Monte Carlo, DSMC)을 사용하는 것이 적절하다. Fig. 1은 누센(Knudsen) 수에 따라 적용할 수 있는 수학적 모델을 나타낸 그림이다. 누센 수가 1보다 매우 작은 영역에서는 유동을 연속체로 가정할 수 있지만, 누센 수가 커지면 유동을 연속체로 가정할 수 없으며, 유동 입자의 운동과 충돌을 각각 모사하는 Boltzman 방정식을 지배방정식으로 사용하는 DSMC 방법을 사용하는 것이 적절하다[6].

Fig. 1

Flow regimes and characteristics according to the local Knudsen number.

로켓 페어링 공력가열 해석에서는 페어링이 분리되기 전까지 페어링에 가해지는 열 유속을 계산해야 한다. CFD 해석은 고도가 높아지면서 밀도가 낮아지고 연속체로 가정하기 어려워지며 해석이 어려워진다. DSMC 해석은 누센 수가 큰 고고도에서 고도가 내려가면서 누센 수가 작아지고 입자 수가 많아져서 해석에 필요한 시간이 증가한다. 따라서, 페어링 공력가열 해석을 할 때, CFD 해석과 DSMC 해석의 전환이 생기는 고도가 발생한다.

본 연구에서는 CFD와 DSMC 해석의 전환이 생기는 고도에서 로켓 페어링의 공력가열 해석을 수행한다. CFD와 DSMC 해석을 수행하여 동일한 고도 조건에서 페어링에 가해지는 열 유속을 계산하고 비교한다.

2. 해석 조건

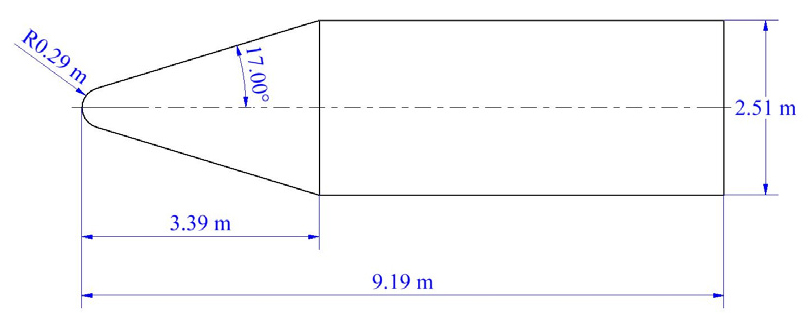
본 연구에서는 CFD와 DSMC를 사용하여 누리호와 엡실론 로켓의 페어링 공력가열 해석을 수행하였다. Fig. 2는 해석에 사용된 엡실론 로켓의 페어링 형상이며 누리호 로켓은 직경이 2번 바뀌는 점을 제외하고 이와 유사하다. 해당 형상을 가지고서 2차원 축대칭 해석을 수행하였다.

Fig. 1을 보면 누센 수가 10^-3보다 커지면 희박해지기 시작한다. 누리호와 엡실론 로켓의 누센 수는 80 km에서 각각 1.97×10-3와 2.04×10-3이며 고도가 올라감에 따라 증가한다. 따라서, 누리호와 엡실론 로켓의 비행에서 80 km 고도일 때 CFD와 DSMC 해석을 수행하였다. 80 km 공기 조건은 U.S. Standard Atmosphere[7]를 참고하였으며 해석에 사용한 조건들을 Table 1에 정리하였다.

Fig. 2

Fairing shape of the Epsilon.

3. CFD 해석

3.1 CFD 해석 모델

로켓 페어링의 CFD 해석은 여러 선행연구[8,9,10]에서 수행되었다. 선행연구들을 기반으로 해석 모델을 선정하였다. 선정한 해석 모델은 Table 2에 정리하였다. Table 2에 정리한 해석 모델을 가지고 C-type 모양 도메인에서 해석을 수행하였으며 도메인의 크기는 페어링의 10배 이상이다.

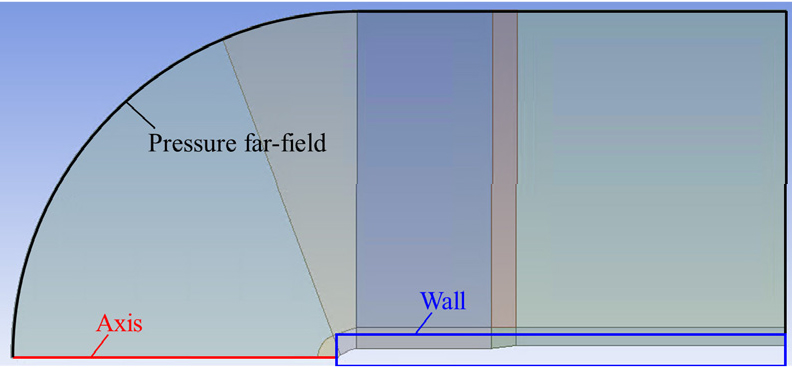
Fig. 3은 해석에 사용한 경계 조건을 나타낸 그림이다. 해석 도메인의 경계 중 외부 유동이 들어오고 나가는 곳은 pressure far-field 경계 조건으로 설정하였다. 이는 압력 값을 특정하는 것이 아니라 게이지 압력을 0으로 두고 마하수, 온도, 난류 조건을 경계 조건으로 설정한다. 따라서, 해당 경계에서 유체가 특정 방향, 특정 마하수로 들어오고 나가는 것으로 설정하였다. 페어링과 로켓 동체로 이루어져 있는 벽면은 등온 300 K 점착(no slip) 조건으로 설정하였다.

Fig. 3

CFD boundary condition.

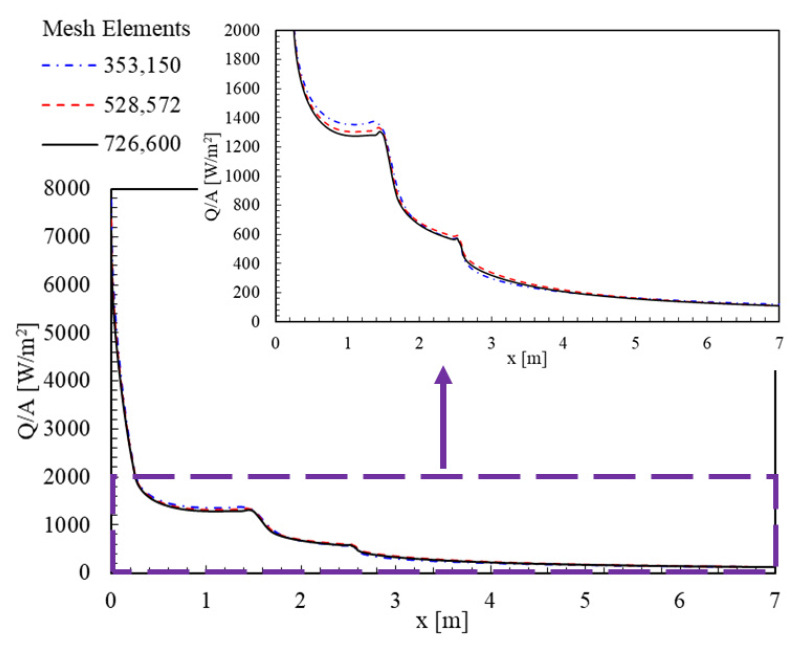
선정한 해석 모델과 경계 조건을 가지고서 누리호 페어링 형상에 대하여 격자 수렴 분석을 진행하였다. 격자 수렴 분석은 총 격자 개수가 353,150개, 528,572개, 726,600개인 세 가지 격자에 대하여 수행하였다. 세 가지 격자로 해석한 페어링 벽면에 가해지는 열 유속을 Fig. 4에 나타내었다. Fig. 4를 보면, 세 가지 격자로 해석하였을 때, 열 유속의 결과가 유사하다. Fig. 4에서 확대한 결과를 보았을 때, 격자의 개수가 늘어나면서 결과의 차이가 작아졌다. 353,150개 격자와 528,572개 격자의 x = 1.02 m에서의 결과는 48.40 W/m²(3.7%) 차이가 났으며 528,572개 격자와 726,600개 격자의 x = 1.02 m 에서의 결과는 27.92 W/m²(2.2%) 차이가 났다.

Fig. 4

Nuri heat flux results by using various mesh elements.

세 가지 격자로 해석하였을 때, 정체점에서의 열 유속 결과를 Table 3에 정리하였다. 이를 보면, 격자의 개수가 증가할수록 열 유속이 감소한다. 누리호와 엡실론 로켓의 페어링의 노즈콘 모양은 구 모양이다. Thauber, M.E.[11]는 극초음속 유동에서 구의 정체점에서의 열 유속을 반지름, 자유 유동의 밀도, 자유 유동의 속도로 정의하였으며 해당 식은 Eq. 1이다.

Eq. 1에서 (1-hw/h0) 항은 hot wall correction으로 극초음속 유동에서 hw≪h0이므로 1로 근사할 수 있다. 누리호의 노즈콘 반지름은 0.45 m이고 80 km 조건에서 자유 유동의 밀도는 1.84×10-5 kg/m³, 자유 유동의 속도는 1,861 m/s이다. 이 조건들을 Eq. 1에 대입하여 계산한 80 km 조건에서 누리호 정체점에서의 열 유속은 7,545 W/m²이다. 계산 식 결과와 CFD 해석 결과의 오차율을 Table 3에 정리하였다. 계산 식과 차이는 528,572개 격자를 사용하였을 때 2.45%로 가장 작았다. 따라서, 80 km 조건의 열 유속을 가장 잘 예측하는 격자를 528,572개 격자로 판단하였으며 이후 누리호의 CFD 해석 결과는 528,572개 격자를 사용한 결과이다. 또한, 엡실론 로켓 해석은 누리호 격자를 생성할 때와 동일한 방법을 사용하였고 격자의 개수가 누리호 격자와 유사한 535,337개의 격자를 사용하여 해석을 수행하였다.

3.2 CFD 해석 결과

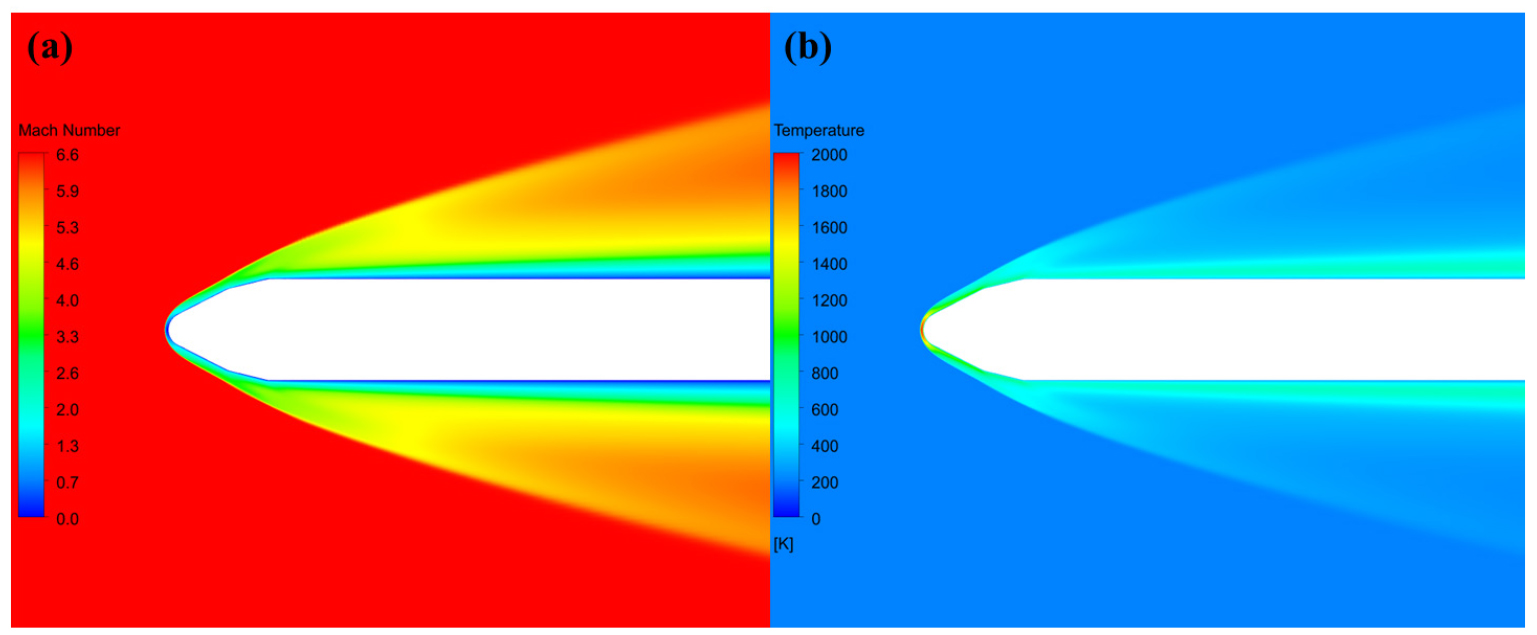
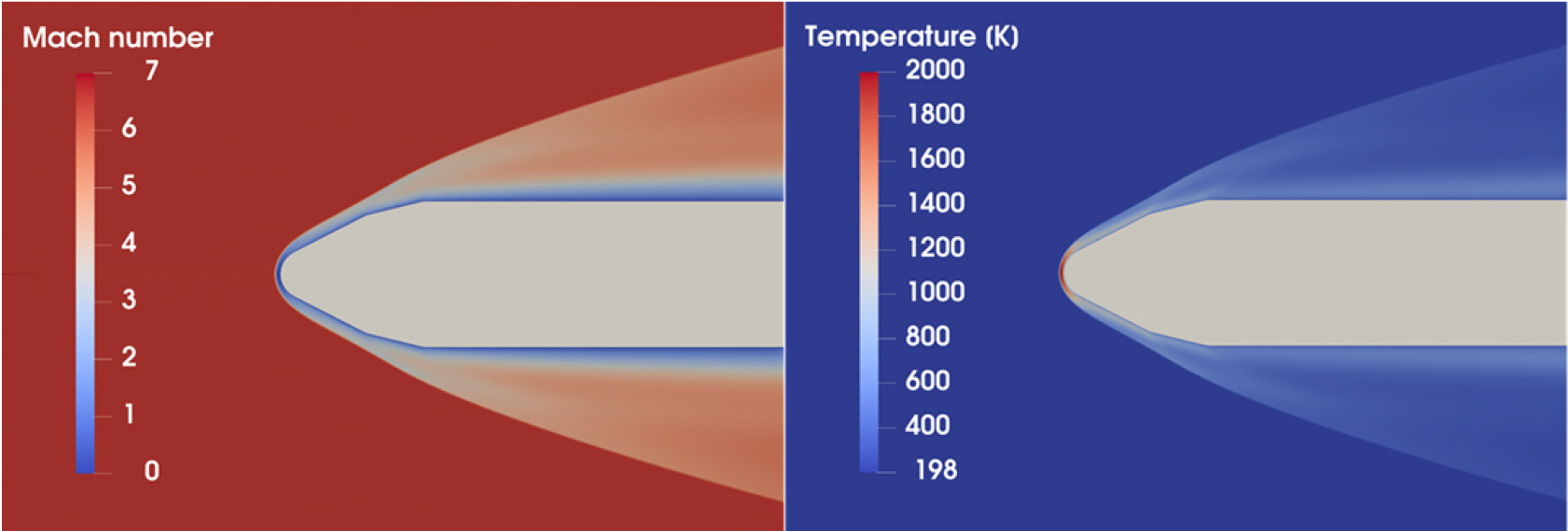
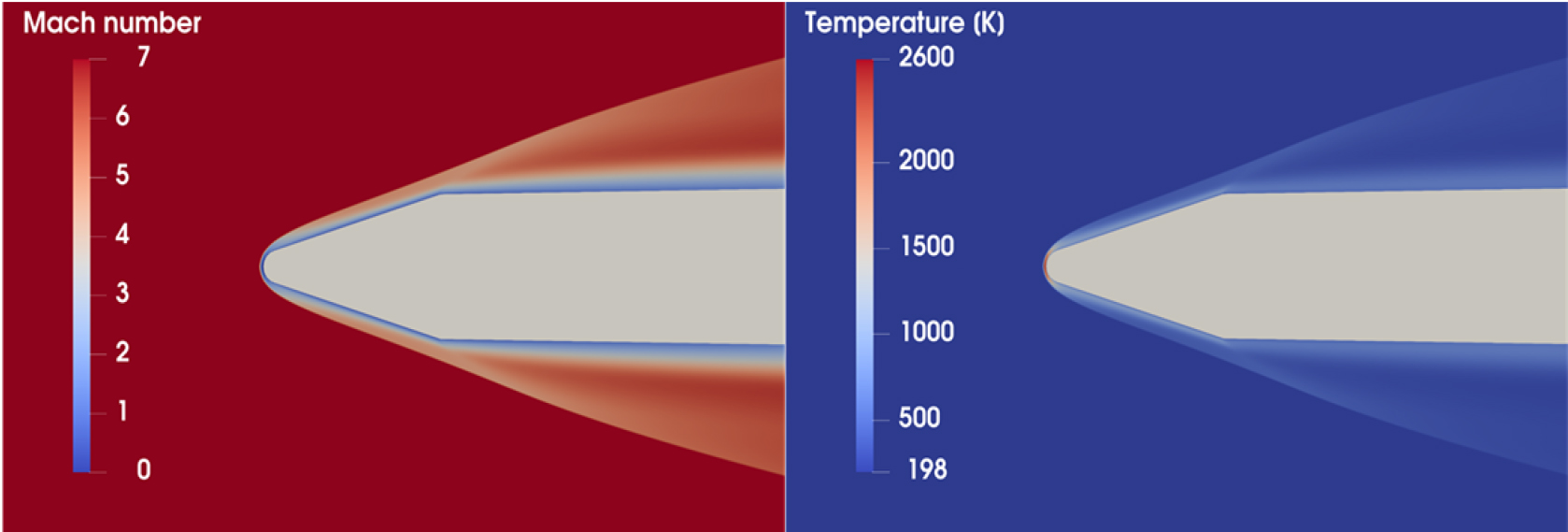
Fig. 5와 Fig. 6은 각각 누리호와 엡실론 로켓의 마하수 분포와 온도 분포 그림이다. 누리호와 엡실론 로켓 모두 충격파가 노즈콘을 만나며 형성되었다. 온도의 최댓값은 정체점 근처에서 형성되었으며 누리호는 1,914 K, 엡실론 로켓은 2,327 K으로 계산되었다.

Fig. 5

CFD results of the Nuri: (a) Mach number and (b) Temperature.

Fig. 6

CFD results of the Epsilon: (a) Mach number and (b) Temperature.

4. DSMC 해석

4.1 DSMC 해석 모델

DSMC는 Boltzmann 방정식의 현상학적인 수치 해를 제공하는 방법론으로 1960년대 G.A. Bird가 개발하였다[6]. Boltzmann 방정식은 Eq. 2로 표현된다.

여기서 n은 수밀도, F는 외력, c→는 속도 벡터, r→은 위치 벡터, (f,f1)은 충돌 전의 속도 분포함수, (f*,f1*)은 충돌 후의 속도 분포함수, cr은 충돌하는 두 입자 쌍의 상대 속도 크기, σ는 충돌 단면적, Ω는 충돌 후 입자의 방향이다. Boltzmann 방정식의 좌변은 입자의 이동을 기술하고, 우변은 입자 간의 이중 충돌을 기술한다[12,13].

DSMC 방법은 해석 영역 내에 여러 개의 계산 입자를 생성한다. 하나의 계산 입자는 많은 수의 현실 기체를 대표할 수 있다. 계산 입자를 사용하여 한 시간 간격 내에 입자의 이동과 충돌과정을 확률적으로 구현한다. 계산 입자가 많아질수록 통계적 에러를 낮출 수 있지만, 그로 인한 계산비용이 증가할 수 있다. 통상적으로 격자당 최소 10개 이상의 계산 입자가 권고되며, 본 연구에서는 격자당 20개 이상의 계산 입자를 사용하였다. 온도와 같은 유동의 거시적인 물성치는 속도 분포 함수에 평균을 취해 얻을 수 있다. 로켓 페어링의 DSMC 해석을 위해 SPARTA 코드를 사용하였다[14]. SPARTA는 미국의 정부출연 연구소인 Sandia Lab에서 개발된 DSMC 코드로 2014년에 공개되었다.

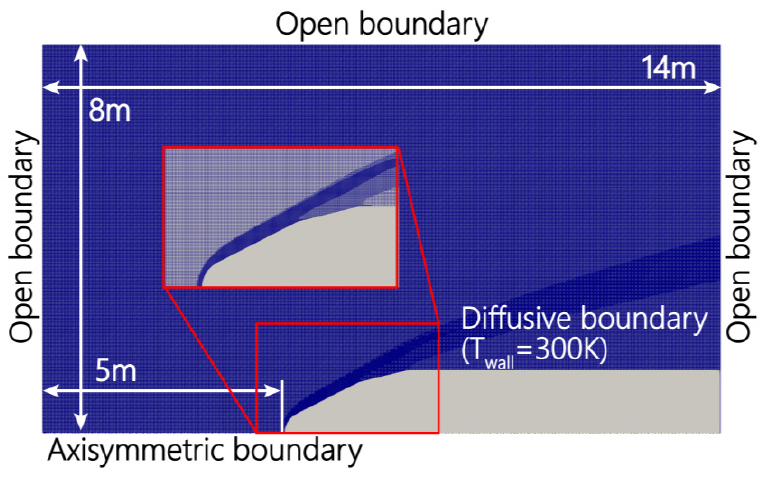
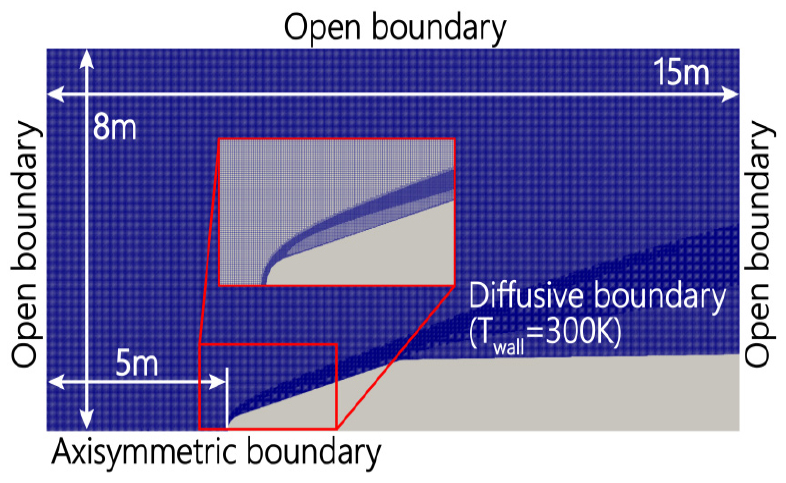
Fig. 7과 Fig. 8은 각각 누리호와 엡실론 로켓 해석에 사용한 계산 영역과 경계 조건이다. 왼쪽 경계면으로 유동이 들어오는 조건으로 왼쪽과 오른쪽 그리고 상단의 경계면은 열린 경계면으로 설정하였다. 축대칭 형상으로 해석하기 위해 x축을 기준으로 축대칭 조건을 적용하여 해석하였다. 로켓 동체로 구성된 벽면은 300 K의 등온 조건을 가정하였으며 난반사 경계 조건을 적용했다.

DSMC를 사용하여 정확한 해석 결과를 얻기 위해서는 격자의 크기를 평균자유행로보다 작게 설정해야 한다. 균일한 격자를 사용하면 격자 크기는 밀도가 가장 높은 영역을 기준으로 격자 크기를 설정할 필요가 있다. 이러한 접근법은 결과적으로 불필요하게 많은 계산 격자를 요구한다. 따라서 본 연구에서는 유동의 국소적인 평균자유행로에 따라 격자 크기를 다르게 사용하기 위해 적응형 격자 기법을 사용하였다. Fig. 7과 Fig. 8에서 각각 누리호와 엡실론 로켓 해석에 사용된 격자를 확인할 수 있다.

DSMC를 사용하여 정확한 해석 결과를 얻기 위해서는 시간 간격의 크기를 평균충돌시간보다 작게 설정해야 한다. 고도 80 km에서 평균충돌시간은 9.5×10-6 s로 누리호와 엡실론 로켓 해석에는 이보다 작은 1.0×10-6 s를 사용해 해석하였다.

Fig. 7

DSMC computation domain and boundary condition for Nuri.

Fig. 8

DSMC computation domain and boundary condition for Epsilon.

4.2 DSMC 해석 결과

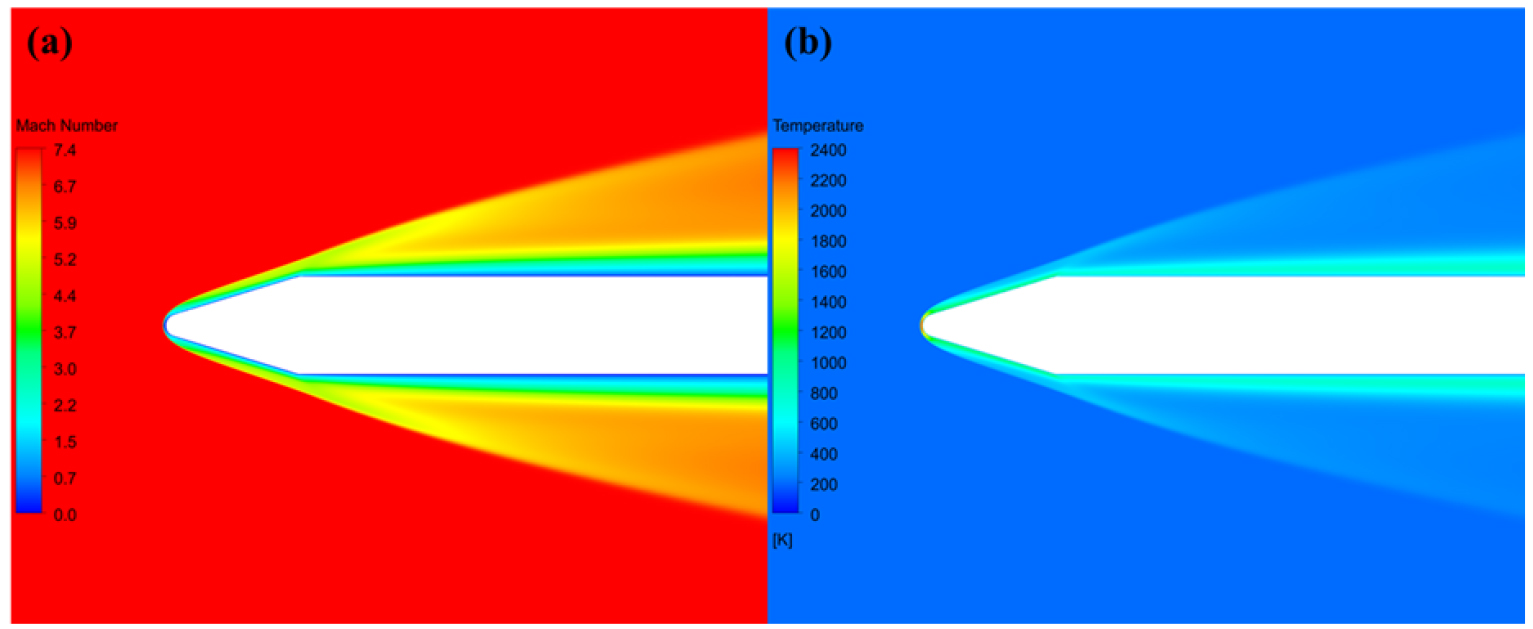
Fig. 9와 Fig. 10은 각각 누리호와 엡실론 로켓의 마하수 분포와 온도 분포 그림이다. 누리호와 엡실론 로켓 모두 CFD 해석과 동일하게 노즈콘 전방에 충격파가 형성되었다. 온도의 최댓값은 정체점 근처에서 형성되었으며 누리호는 1,953 K, 엡실론은 2,375 K으로 계산되었다.

Fig. 9

DSMC results of the Nuri: (a) Mach number and (b) Temperature.

Fig. 10

DSMC results of the Epsilon: (a) Mach number and (b) Temperature.

5. CFD와 DSMC 해석 결과 비교

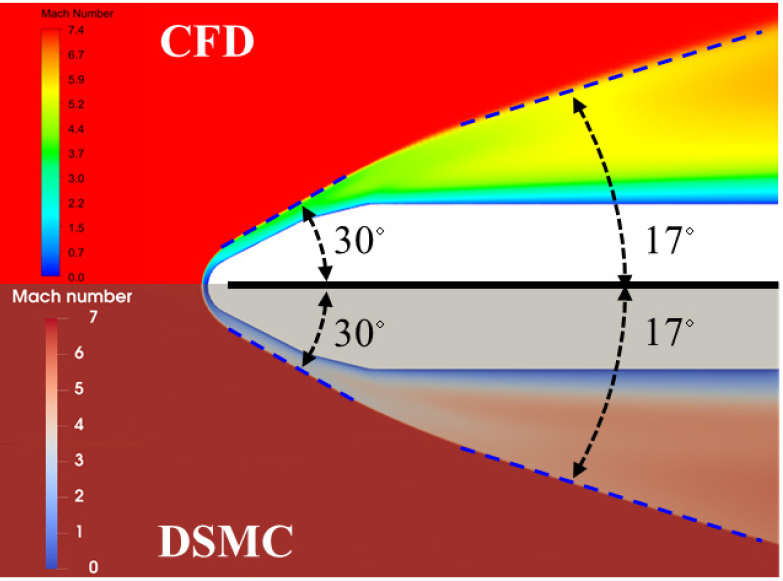
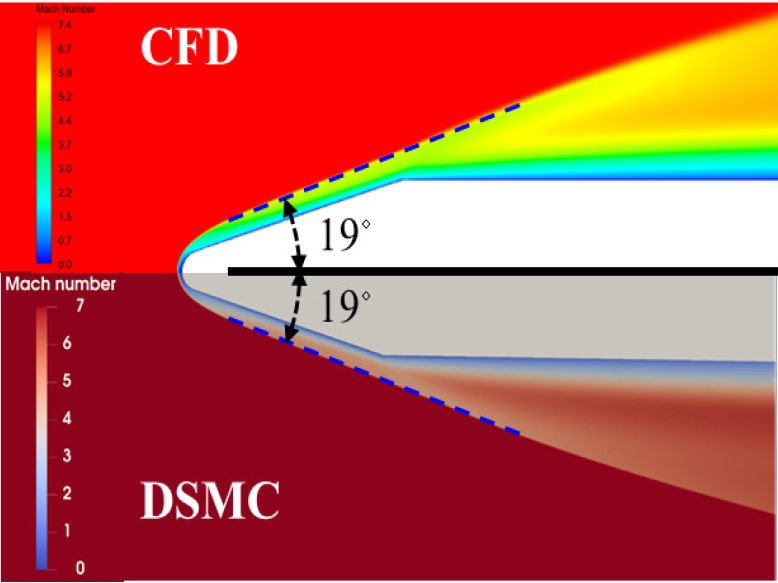
Fig. 11과 Fig. 12는 각각 누리호와 엡실론 로켓의 마하수 분포 해석 결과를 비교한 것이다. Fig. 11의 누리호 해석 결과를 보면, CFD와 DSMC로 해석한 충격파가 거의 유사하다. CFD와 DSMC 해석에서 모두 충격파의 기울기는 정체점 근처를 제외하고 한 번 변화한다. 충격파의 각도도 CFD와 DSMC에서 모두 30°와 17°로 동일하였다. Fig. 12의 누리호 해석 결과에서도 CFD와 DSMC로 해석한 충격파가 거의 유사하다. 충격파의 각도도 CFD와 DSMC에서 모두 19°로 동일하였다.

Fig. 11

Comparison of CFD and DSMC Mach number results of the Nuri.

Fig. 12

Comparison of CFD and DSMC Mach number results of the Epsilon.

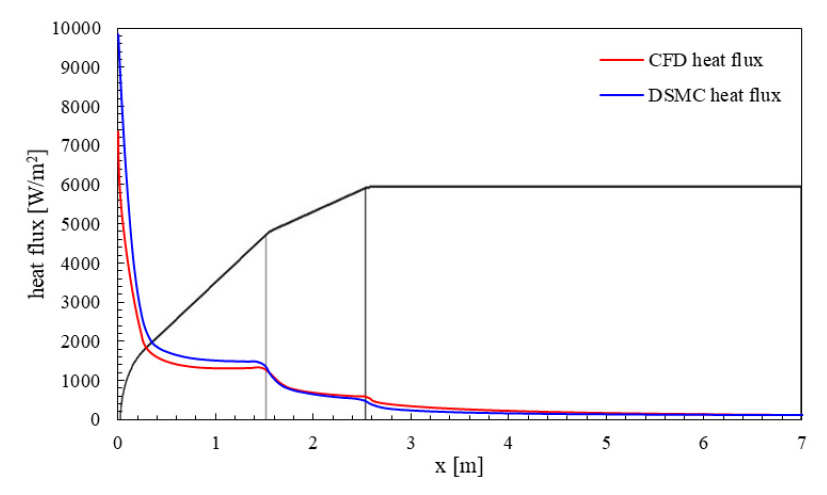
CFD와 DSMC로 해석한 누리호 페어링 벽면에 가해지는 열 유속을 페어링의 모양과 함께 Fig. 13에 나타내었다. 두 방법으로 계산한 열 유속은 정체점 부근을 제외하고 약 1.5 m 구간부터 유사하였다. 정체점에서의 열 유속은 CFD와 DSMC에서 각각 7,360 W/m², 9,827 W/m²이다. 해당 값을 Eq. 1을 이용하여 계산한 열 유속과 함께 Table 4에 나타내었다.

Fig. 13

Nuri heat flux results by using CFD and DSMC.

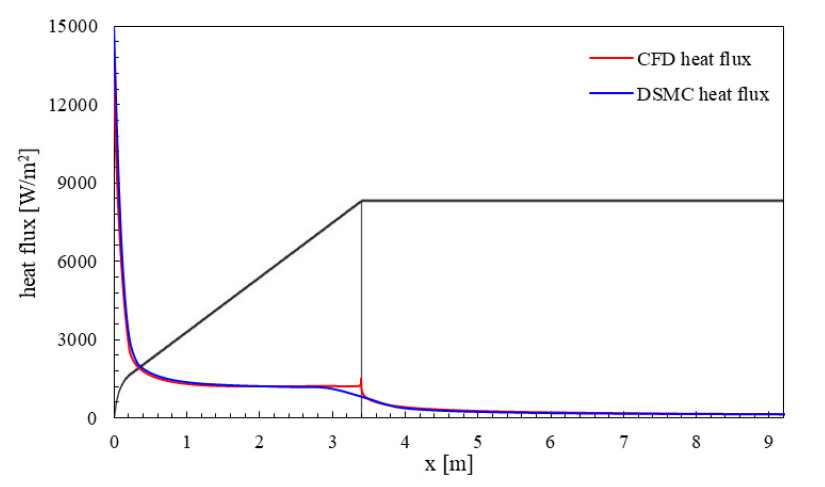
CFD와 DSMC로 해석한 엡실론 로켓 페어링 벽면에 가해지는 열 유속을 Fig. 14에 나타내었다. 두 방법으로 계산한 열 유속은 정체점 근처를 제외하고 유사하였다. 정체점에서의 열 유속은 CFD와 DSMC에서 각각 14,098 W/m², 15,086 W/m²이다. 해당 값을 Eq. 1을 이용하여 계산한 열 유속과 함께 Table 5에 나타내었다.

Fig. 14

Epsilon heat flux results by using CFD and DSMC.

CFD와 DSMC 모두 Eq. 1의 열 유속보다 더 크게 예측하였다. Eq. 1의 결과와는 CFD의 결과가 DSMC의 결과보다 유사하였다. Eq. 1이 산출된 유동의 압력 범위는 1.0×102 ~ 1.0×106 Pa(수밀도는 3.69×1022 kg/m³ ~ 3.69×1026` kg/m³)이다[15]. 해당 압력은 대략 고도 40 km 압력에서 지구 표면 압력의 10배에 해당하는 범위이다. 이 압력과 밀도 범위는 CFD가 잘 재현할 수 있는 것으로 알려져 있다. 본 연구에서 해석 목표로 한 고도 80 km 압력은 1.05 Pa(3.84×1020 kg/m³)로 Eq. 1의 최저 압력 범위보다 100배 이상 작은 압력 조건을 가진다. 이러한 저밀도·저압력 비평형 유동에서는 Eq. 1이 적용되지 않을 수 있다. 또한, CFD는 충격파와 같은 비평형 유동 현상의 열 유속을 과소 예측할 수 있다고 보고된 바 있다[16,17].

6. 결 론

탑재체를 보호하기 위한 로켓 페어링의 적절한 열보호 설계를 위해서 페어링에 가해지는 열 유속을 정확히 예측하여야 한다. 고도에 따라서 공기의 밀도가 달라지며 공기의 밀도가 높은 고도에서는 CFD 해석, 낮은 고도에서는 DSMC 해석으로 열 유속을 예측한다. 이로 인하여 CFD와 DSMC 해석의 전환이 발생하는 고도가 발생한다. 따라서, 본 연구에서는 80 km 고도 조건(누센 수: 약 2.0×10-3)에서 누리호와 엡실론 로켓의 페어링에 대해 CFD와 DSMC 해석을 수행하였고 그 결과를 비교하였다.

CFD와 DSMC로 누리호와 엡실론 로켓을 해석하였을 때 예측되는 충격파의 형상은 전반적으로 유사하였다. 두 해석 모두 정체점 근처 부근에서 최대 온도를 예측하였다. 누리호 해석에서는 CFD와 DSMC 해석에서 각각 1,914 K, 1,953 K을 예측하였다. 엡실론 로켓 해석에서는 CFD와 DSMC 해석에서 각각 2,327 K, 2,375 K을 예측하였다. CFD와 DSMC 해석에서 최대 온도의 차이가 누리호와 엡실론 로켓 해석에서 모두 2.0%로 비슷하였다.

CFD와 DSMC 해석으로 계산한 페어링 벽면에 가해지는 열 유속은 정체점 근처를 제외하고 유사하였다. 구의 정체점에서의 열 유속 식(Eq. 1)의 계산 값과는 CFD 해석에서 계산한 정체점에서의 열 유속이 더 유사하였다.

80 km 고도 조건에서 누리호와 엡실론 로켓의 페어링에 가해지는 공력가열을 해석하였을 때, CFD와 DSMC 해석이 비교적 유사하게 예측되었다. 따라서, 상승하는 로켓의 페어링 해석에서 누센 수가 약 2.0×10-3인 고도를 전환 고도로 선정하는 것이 적절한 것으로 보인다.