Conceptual Design and System Analysis of 10 kN Nuclear Thermal Propulsion Engine

Soo Seok Yang; Namkyung Cho; Si-Yoon Kang; Jeong-Yeol Choi

doi:10.6108/KSPE.2024.28.4.029

Preview

RESEARCH PAPERS

Journal of the Korean Society of Propulsion Engineers. 31 August 2024. 29-38
https://doi.org/10.6108/KSPE.2024.28.4.029

Conceptual Design and System Analysis of 10 kN Nuclear Thermal Propulsion Engine

10 kN 원자력 열추진 엔진의 개념설계 및 시스템 해석

Soo Seok Yang^a^*

Namkyung Cho^a

Si-Yoon Kang^b

Jeong-Yeol Choi^b

양 수석^a^*

조 남경^a

강 시윤^b

최 정열^b

^aKorea Aerospace Research Institute, Korea

^bDept. of Aerospace Engineering, Busan National University, Korea

^{*Corresponding Author}

The Korean Society of Propulsion Engineers

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

For Mars exploration, the development of nuclear thermal propulsion engines has been attempted since the 1970s, mainly in the United States, and the development is currently underway at NASA. In this study, the conceptual design and system analysis of a nuclear thermal propulsion engine with a thrust of 10 kN and a specific thrust of 950 seconds are performed, which can be used as a propulsion engine for a Mars exploration spacecraft. The reactor uses low-enriched UN nuclear fuel with a heat capacity of 54 MW manufactured in the form of TRISO. The engine consists of an expander cycle using hydrogen as a propellant. To supply hydrogen, an integrated turbopump consisting of a 301 kW hydrogen pump and turbine are used. The nozzle shape is designed as a parabolic bell nozzle with a choking area of 13.8 cm², a contraction ratio of 250, and a expansion ratio of 550. The regenerative cooling design and analysis of the nozzle are performed to improve the reliability of the system analysis. As a result of the system analysis, it is confirmed that the conditions of a total temperature of 2850 K and a total pressure of 4.41 MPa are appropriately formed at the engine thrust chamber to meet the required performance of the nuclear thermal propulsion engine.

Keywords

Nuclear Thermal Propulsion(NTP)

Expander Cycle

Hydrogen Pump

UN Reactor

Regenerative Cooling

화성 탐사를 위해서 1970년대부터 미국을 중심으로 원자력 열추진 엔진의 개발이 시도되었으며, 현재 NASA에서 개발이 진행되고 있다. 본 연구에서는 화성 탐사용 우주선의 추진기관으로 사용 가능한 추력 10 kN 및 비추력 950 초의 원자력 열추진 엔진의 개념설계 및 시스템 해석을 수행하였다. 원자로는 열용량 54 MW의 저농축 UN 핵연료를 TRISO 형태로 제작하여 사용한다. 엔진은 팽창기 사이클로 구성하며 수소를 추진제로 사용한다. 수소를 공급하기 위하여 301 kW급의 수소 펌프 및 터빈으로 구성된 일체형 터보 펌프를 사용한다. 노즐의 형상은 목 면적 13.8 cm², 수축비 250 및 확장비 550의 포물선형 벨 노즐로 설계한다. 수소를 사용한 노즐의 재생 냉각 설계 및 해석을 수행하여 시스템 해석의 신뢰도를 높였다. 시스템 해석 결과, 원자력 열추진 엔진의 요구 성능을 만족시키기 위하여 엔진 추력실의 전온도 2850 K 및 전압력 4.41 MPa가 적정하게 형성됨을 확인하였다.

키워드

원자력 열추진

팽창기 사이클

수소 펌프

UN계열 원자로

재생냉각

MAIN

1. 서 론
2. 시스템 개념설계
2.1 원자로 설계
2.2 노즐형상 설계
2.3 재생냉각 설계
2.4 터보펌프 설계
3. 시스템 해석
3.1 “1 → 2” 구간
3.2 “2 → 3” 구간
3.3 “3a → 5a” 구간
3.4 “3b → 5b” 구간
3.5 “6 → 7 → 8” 구간
3.6 “8 → 9” 구간
4. 시스템 해석 결과
5. 결 론

Nomenclature

$I_{s}$ : specific impulse

$F$ : thrust

$g_{c}$ : acceleration of gravity

$A_{e}$ : nozzle exit area

$L_{n}$ : nozzle length

$R_{t}$ : radius of nozzle throat

$A_{c}$ : nozzle chamber area

$H$ : overall heat transfer coefficient

$t_{w}$ : nozzle wall thickness

$k_{w}$ : conductivity of nozzle wall

$C_{p}$ : constant pressure heat capacity

$μ$ : viscosity

$P_{r}$ : prandtl number

$ρ$ : density of H₂ gas at nozzle inside

$u$ : velocity of H₂ gas at nozzle inside

$k_{c f}$ : coolant conductivity at film condition

$D_{c}$ : hydraulic diameter of coolant tube

$ϕ_{c u r v e}$ : correction term for curvature effect

$W_{t}$ : turbine work

1. 서 론

1960년대 달 착륙을 위한 로켓 개발이 진행되고 있을 당시에 미국은 달을 넘어서 화성 유인탐사라는 거대한 계획도 함께 계획하고 있었다. 이때 화성 유인탐사를 위해서 개발된 엔진이 원자력 열추진 엔진인 Nuclear Engine for Rocket Vehicle Application(NERVA)이다.

NERVA 엔진은 지상에서의 시험까지 개발이 진행되었지만, 당시 베트남 전쟁 및 미국 경제의 어려움으로 닉슨 행정부는 NASA의 예산을 대폭 삭감하면서 NERVA 개발은 1972년에 중단되었다[1].

당시 NERVA의 기술 사양은 추력이 1,000 kN급의 대형 엔진이며 비추력이 850 초, 추력/무게비가 3정도였다. 네바다 사막에서 시험으로 입증한 엔진 성능은 추력 250 kN으로 28분간 운전한 결과, 비추력 710 초의 성능을 보였다[1,2].

당시에 원자력 열추진 엔진에 대한 기술은 구소련도 상당한 수준의 기술을 가지고 있었던 것으로 알려져 있다[3]. NERVA 엔진의 개발이 중단된 이후부터 1980년대까지는 관련 기술의 진전이 거의 없었으나, 1990년부터 미국의 원자력 국립연구소 등에서 원자력 열추진 엔진에 대한 연구들이 다시 진행되기 시작하였다. 미 공군이 주도한 Space Nuclear Thermal Propulsion(SNTP) 프로그램에서 Particle Bed Reactor(PBR) 방식의 엔진이 연구되었으며, 프랑스 Centre National D'Etudes Spatiales(CNES)도 Moteur atomique pour l'espace Propulsion(MAPS) 프로그램에서 원자력 열추진 엔진을 연구하였고, 미국의 브룩헤이븐 국립연구소는 Miniature Reactor Engine(MITEE)라는 초소형 원자력 열추진 엔진을 연구하였다[4,5,6].

이러한 기술의 진전으로 3,000 K 이상의 높은 온도에서 운용되는 핵연료가 현재 개발되고 있으며, 이에 따라 비추력도 1,000 초 이상의 높은 성능을 보이고 있다. 추력/무게비도 NERVA 엔진보다 2배 이상 좋아지고 있으나, 추력은 오히려 작아져서 소형 엔진을 여러개 클러스터링하여 사용하는 추세로 바뀌고 있다[7].

미국은 Advanced Exploration System(AES) 프로그램을 통하여 달에 다시 인간을 착륙시키기 위한 아르테미스 계획을 진행하고 있으며, 달에 이어서 화성으로 사람을 보내는 계획(Mars Design Reference Architecture)도 함께 진행하고 있다[8,9]. 화성의 유인탐사를 위해서는 화석연료 기반이 아닌 새로운 개념의 고효율 추진기관이 반드시 필요하기 때문에 미항공우주국(National Aeronautics and Space Administration, NASA) 은 원자력 열추진 및 원자력 전기추진을 동시에 병행하여 연구하고 있다. 이 프로그램의 일환으로 원자력 열추진 엔진을 개발하기 위한 Nuclear Cryogenic Propulsion Stage(NCPS) 프로젝트가 현재 진행되고 있으며 미국의 BWX Technologies(BWXT), General Atomics(GA) 및 Ultra Safe Nuclear Corporation(USNC) 3개 회사가 NASA와 협력하여 원자력 열추진 엔진 개발에 참여하고 있다[10]. 또한 최근에는 NASA와 Defense Advanced Research Projects Agency(DARPA)의 협력하에 지구 궤도와 달 궤도 사이를 오가는 우주 수송선의 엔진으로 원자력 열추진 엔진을 개발하는 Demonstration Rocket for Agile Cislunar Operations(DARCO) 프로그램이 진행되고 있으며 2026년에 시연을 목표로 하고 있다[11].

전세계적으로 우주탐사에 대한 관심이 커지고 있고, 우주 선진국들은 달뿐 만 아니라 화성에까지 사람을 보내기 위한 계획을 추진하고 있는 추세에 맞추어 국내에서도 우주탐사와 화성의 유무인 탐사를 본격적으로 준비해야 할 것이다. 이를 위해서는 원자력 추진기관에 대한 선행 연구가 반드시 필요하다.

본 연구는 향후 화성탐사선의 추진기관으로 사용 가능한 원자력 열추진 시스템에 대한 개념설계 및 해석을 수행한 결과이다. 원자력 열추진 시스템의 추력은 10 kN으로 설정하여 10 톤급의 무인 탐사선의 추진기관으로 활용할 뿐 만 아니라 향후 유인 탐사선의 추진기관으로 클러스터링하여 활용 가능하다.

2. 시스템 개념설계

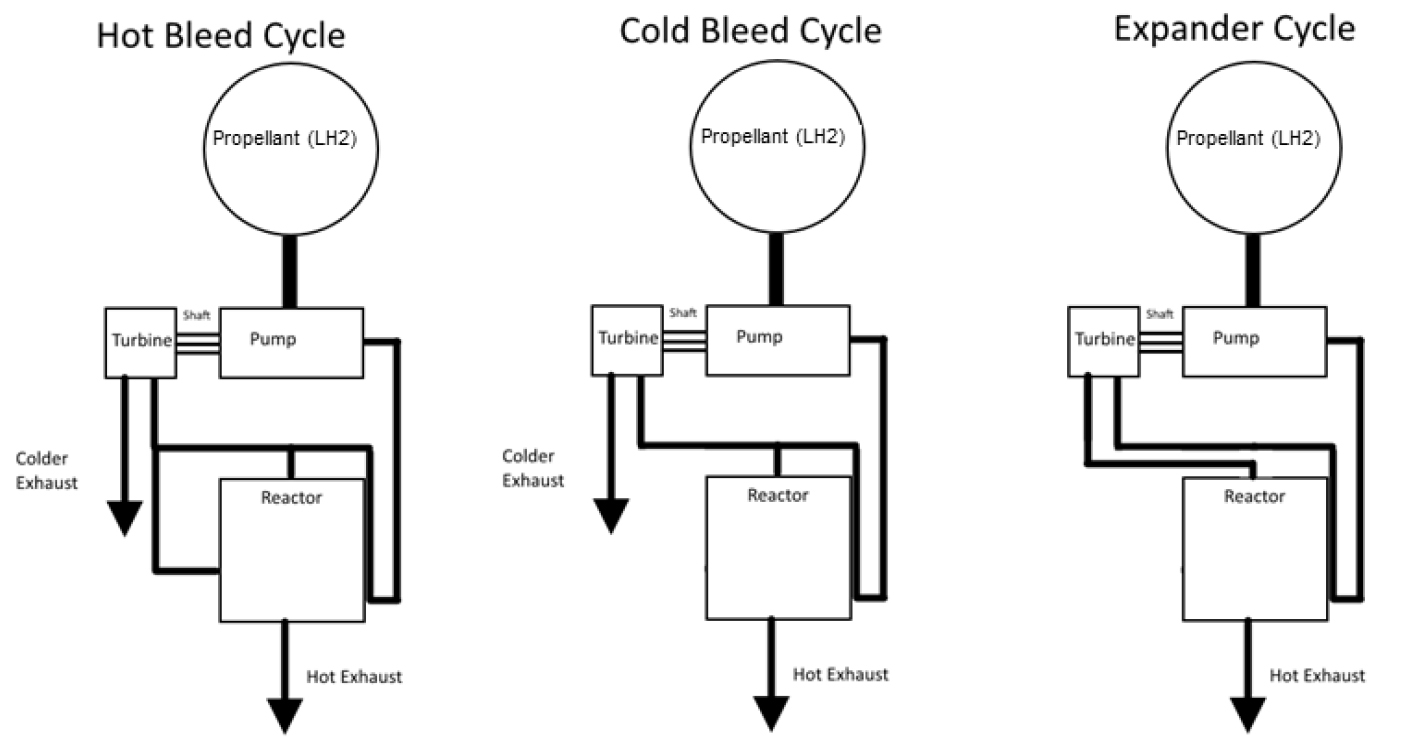
원자력 열추진 시스템은 기존의 화석연료 기반의 로켓 엔진과 형태적으로는 유사하나, 산화제와 연료를 연소시키는 대신에 원자로에서 발생하는 열을 사용하여 추진제를 가열하여 추력을 발생하는 엔진이다. 원자력 열추진 엔진의 사이클은 Fig. 1과 같이 3가지 종류로 구분되며, 엔진의 추력, 비추력, 신뢰성 및 복잡성 등이 사이클에 따라 조금씩 달라지기 때문에 사용 목적에 맞추어 결정해야 한다. 본 연구에서는 신뢰성이 높으면서도 비추력이 비교적 좋은 팽창기 사이클로 결정하여 개념설계를 수행하였다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F1.jpg

Fig. 1

Nuclear thermal engine cycles.

원자로 냉각재로는 여러 물질을 고려할 수 있으나, 작은 분자량으로 인하여 가장 큰 비추력을 얻을 수 있는 수소가 원자력 열추진의 장점을 살릴 수 있는 유일한 추진제로 여겨진다. 또한 비열이 크기 때문에 원자로를 냉각시키는데도 효과적이다. 그러나 수소를 가열하는데 많은 열이 필요하기 때문에 원자로의 열용량이 커진다. 또한 작은 밀도 때문에 큰 탱크가 필요하며, 체적 유량이 커짐으로 수소를 이송시키기 위한 배관 등에서의 압력 손실도 커지며, 저온 상태로 장기간 보관하기 위한 기술적 어려움도 있다.

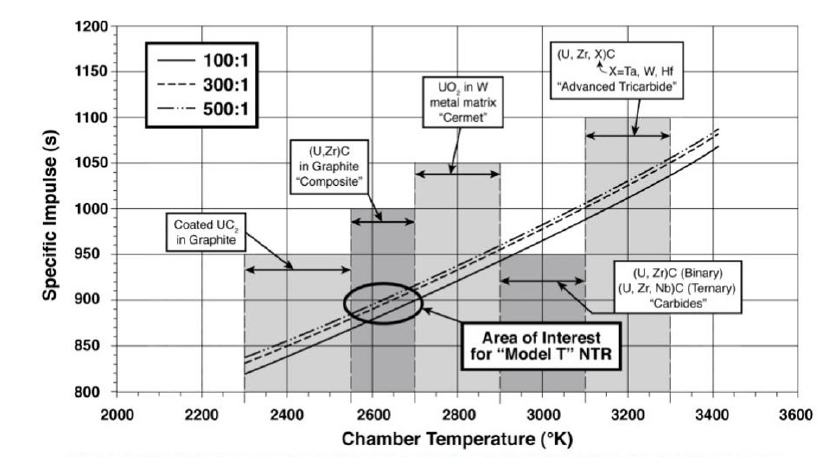
원자력 열추진 시스템의 가장 큰 장점은 가장 작은 분자량을 가지는 수소를 추진제로 이용함으로써, 비추력이 기존의 화석연료 엔진보다 2배 이상 크다는 것이다. 이러한 비추력은 Fig. 2에서와 같이 핵연료를 통과하면서 가열된 추진제의 온도에 따라 결정되며, 엔진 추력실의 온도는 핵연료의 종류에 따라 그 범위가 정해진다. NERVA 엔진에서 사용된 (U,Zr)C 복합재 핵연료는 비추력이 900초 이하에서 사용 가능하며, 비추력이 1000초 이상일 경우는 초고온 핵연료의 개발이 필요하다[12]. 본 연구에서는 목표 비추력을 950초로 설정하였으며, 이에 따라 엔진 추력실 온도는 2850 K 이상이 되어야 한다. 따라서 이와 같이 높은 설계 온도에서도 충분히 운용 가능한 핵연료를 사용하여 원자로의 개념설계를 수행하였다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F2.jpg

Fig. 2

Specific impulse depending on nuclear fuel.

2.1 원자로 설계

본 연구의 원자로는 농축도 19.75 wt%의 저농축 Uranium Mononitride(UN) 핵연료를 삼중피복입자핵연료 (TRi- structural ISOtropic, TRISO) 형태로 사용하는 것을 기본으로 한다. TRISO 핵연료의 경우, 기존의 고체 핵연료보다 온도에 잘 견디는 장점이 있으나 부피가 커질 수 있는 단점이 있다. 따라서 버퍼층의 두께를 최소화하면서도 안전에 영향을 주지 않도록 최적화하는 설계가 필요하다.

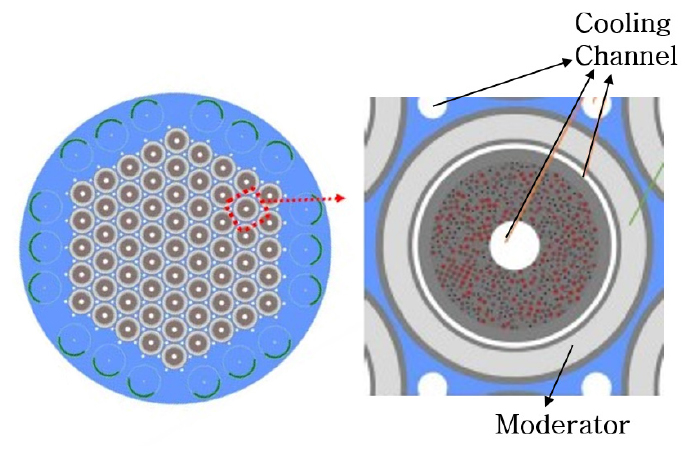
원자로의 구성은 Fig. 3과 같이 흑연 매트릭스로 만들어진 TRISO 핵연료와 핵연료를 둘러싸고 있는 ZrH_1.66 감속재가 하나의 연료봉으로 구성된다. 원형의 원자로 내에는 이러한 연료봉이 여러개 들어가게 되고 연료봉 주위는 BeO 반사체가 둘러싸고 있고, 가장 외곽에는 운전 및 정지를 위한 제어드럼이 설치되어 있다. 제어드럼의 한쪽 면에는 B₄C 흡수체가 있어서 이것으로 원자로의 반응을 활성화 혹은 정지시킬 수 있다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F3.jpg

Fig. 3

Nuclear reactor and fuel.

핵연료 매트릭스 중앙, 핵연료와 감속재 사이, 그리고 반사체에는 냉각을 위한 채널이 있어서 추진제인 수소가 지나간다. ZrH_1.66 감속재는 1000 K 이상에서는 수소 누출이 생길 수가 있기 때문에 냉각이 필요하다. 감속재와 반사체의 냉각 채널을 지난 수소는 터보펌프의 터빈을 구동시키고 난 뒤에 최종적으로 핵연료 매트릭스 중앙에 있는 채널을 통과하면서 2850 K 까지 가열되어 엔진 추력실로 들어간다.

원자로의 열출력은 50 MW 이상이며, 이를 바탕으로 개념 설계된 원자로의 크기는 외경 66 cm 및 높이 70 cm의 원형이고 무게는 567 kg이다[13]. 현재 개념 설계된 원자로의 크기와 무게는 타 연구결과와 비교할 때 다소 크고 무거운 결과를 보이므로 계속적인 설계 개선이 필요하다.

2.2 노즐형상 설계

핵연료를 통과하면서 가열된 수소는 엔진 추력실을 거쳐서 노즐 목을 지나고 팽창되면서 가속이 되어 추진력을 발생한다. 추진제인 수소의 유량은 목표 추력 10 kN 및 비추력 950초를 만족해야 하므로 Eq. 1로 계산을 하면 1.074 kg/s가 된다.

(1)

I_{s} = \frac{F}{g_{c} {\dot{m}}_{j}}

노즐의 목에서 유동은 질식(choked) 상태가 되므로 유동 관계식인 Eq. 2에 따라 노즐의 목 면적은 엔진 추력실의 압력과 온도에 따라 결정된다.

(2)

{\dot{m}}_{j} = \frac{P_{c} A_{t} φ}{\sqrt{T_{c}}}

여기에서 유량계수 $φ$ 는 아래 Eq. 3과 같이 유체의 비열비와 가스 상수에 따라 결정된다.

(3)

φ = \sqrt{\frac{γ}{R}} (\frac{2}{γ + 1})^{\frac{γ + 1}{2 (γ - 1)}}

엔진 추력실의 압력 $P_{c}$ 는 4.41 MPa, 온도 $T_{c}$ 는 2850 K로 설계하였으므로, 이 압력과 온도에서의 수소의 물성치인 비열비 $γ$ 는 1.293이며 가스 상수 $R$ 은 4124.5 N·m/kg·K이다. 따라서 Eq. 3으로 유량계수 $φ$ 를 계산하고, 수소의 유량 ${\dot{m}}_{j}$ 는 1.074 kg/s 이므로 Eq. 2에 따라 목 면적 $A_{t}$ 는 13.8 cm²로 계산되고, 목의 직경은 4.2 cm가 된다.

노즐 목에서 마하수가 1이 된 수소 추진제는 노즐의 면적이 확장되면서 가속이 되는데 노즐 출구에서의 마하수와 출구 면적은 Eq. 4 및 Eq. 5에 따라 결정된다.

(4)

M_{e} = \sqrt{\frac{2}{γ - 1} [(\frac{P_{c}}{P_{e}})^{\frac{γ - 1}{γ}} - 1]}

(5)

\frac{A_{e}}{A_{t}} = \frac{1}{M_{e}} [\frac{2}{γ + 1} (1 + \frac{γ - 1}{2} M_{e}^{2})]^{\frac{γ + 1}{2 (γ - 1)}}

이때 노즐 출구에서 완전 팽창이 되기 위해서는 노즐 출구 압력 $P_{e}$ 가 지구 저궤도의 대기압수준(10^-4 Pa)으로 낮아져야 하나, 이럴 경우 노즐의 출구 면적이 너무 커지게 된다. 따라서 출구의 속도가 목표한 추력 10 kN을 발생시킬 때 까지만 팽창을 시킨다. 이 때의 추력은 Eq. 6과 Eq. 7에 따라 계산된다.

(6)

F = {\dot{m}}_{j} u_{j} + (P_{e} - P_{a}) A_{e}

(7)

u_{j} = \sqrt{\frac{2 γ R T_{c}}{γ - 1} [1 - (\frac{P_{e}}{P_{c}})^{\frac{γ - 1}{γ}}]}

따라서 노즐의 출구 마하수 $M_{e}$ 가 8.77일 때 추력은 10 kN이 되며, 이 때 노즐 출구 면적비 $A_{e} / A_{t}$ 는 Eq. 5에 따라 550이 된다. 따라서 노즐 출구 면적은 0.76 m², 노즐 출구 직경은 0.98 m가 된다.

(8)

L_{n} = \frac{R_{t} (\sqrt{\frac{A_{e}}{A_{t}}} - 1) + R_{o} (\sec α - 1)}{\tan α}

노즐의 길이는 원뿔 노즐을 기준으로 가정하여 길이를 구하는 Eq. 8에 따라 계산한다[14]. 이때 노즐 목의 외부 반경 $R_{o}$ 는 목 반경의 1.1배로 하고, 원뿔 반각 $α$ 는 16°로 설정한다. 이렇게 계산된 노즐의 길이는 1.65 m이다.

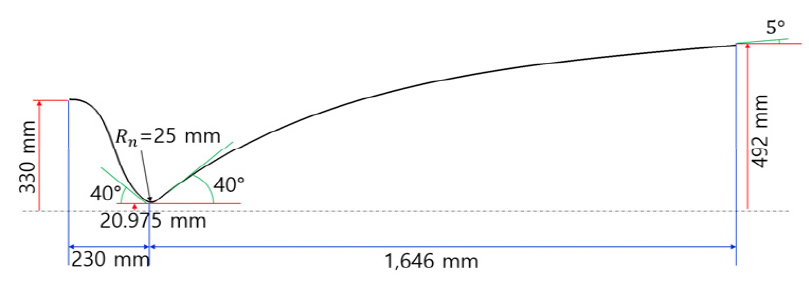
노즐의 형상은 포물선형 벨 노즐로 설정하였고, 포물선 초기 각도는 40°, 노즐 출구 각도는 5°, 노즐 확산부 및 수축부의 곡률 반경은 동일하게 1.2 $R_{t}$ 로 설정하였다. 엔진 추력실의 수축비( $A_{c} / A_{t}$ )는 설계된 핵연료의 크기에 따라 250으로 정하였다. 이와 같이 개념설계 단계에서 결정된 노즐의 형상을 나타내면 Fig. 4와 같다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F4.jpg

Fig. 4

Layout of engine nozzle.

2.3 재생냉각 설계

수소 탱크에서 20 K 정도의 극저온 상태로 저장된 수소는 원자력 열추진 엔진의 노즐 및 원자로의 냉각에 중요한 냉각제로 사용된다. 본 연구의 열추진 엔진은 Fig. 1에서 설명한 바와 같이 팽창기 사이클이기 때문에 펌프를 통과한 수소의 일부는 노즐의 재생 냉각에 사용되고 나머지 수소는 원자로의 내부 냉각에 사용된다. 어느 정도의 수소를 노즐 재생 냉각에 사용할 것인가는 노즐 및 원자로의 냉각에 대한 상세 해석을 통하여 최종적으로 결정될 것이나, 개념설계 단계에서는 1차원 냉각 해석을 통하여 초기 설계값을 설정한다.

재생냉각을 위한 수소는 노즐 확산부의 직경이 약 30 cm 정도가 되는 지점에서부터 유입되어 노즐 목 방향으로 흐르면서 상류 쪽의 노즐 확산부, 노즐 목 그리고 엔진 추력실의 벽을 차례로 냉각시키고 난 뒤에 원자로의 외부 벽을 마지막으로 냉각하고, 원자로의 내부 냉각에 사용된 수소와 합쳐져서 터빈으로 유입된다. 노즐 내부의 고온가스로부터 냉각 유로의 냉각 유체로 전달되는 열전달에 관계하는 복합열전달계수는 Eq. 9와 같이 표현된다.

(9)

H = \frac{1}{\frac{1}{h_{g}} + \frac{t_{w}}{k_{w}} + \frac{1}{h_{c}}}

여기에서 노즐 내벽의 고온가스의 열전달 계수 $h_{g}$ 는 일반적으로 로켓 엔진의 냉각 계산에서 많이 사용되는 Bartz의 Eq. 10을 사용하여 계산하며, 냉각유로 내벽에서 냉각유체의 열전달 계수 $h_{c}$ 는 Colburn의 Eq. 11을 사용하여 계산한다[14,15].

(10)

h_{g} = 0.026 \frac{C_{p}}{P_{r}^{0.6}} \frac{μ^{0.2}}{D^{0.2}} (ρ u)^{0.8} (\frac{D_{t}}{R})^{0.1}

(11)

h_{c} = 0.023 \frac{k_{c f}}{D_{c}} (\frac{C_{p_{c f}}}{k_{c f} μ_{c f}})^{0.4} (\frac{{\dot{m}}_{c} D_{c}}{A_{c}})^{0.8} ϕ_{c u r v e}

열전달 계수의 계산에서 수소 가스의 물성치는 결과에 매우 큰 영향을 미친다. 수소는 재생냉각 유로에서 초임계 상태이며, 추진제로 사용되는 노즐 내부에서는 가스 상태이므로 온도와 압력에 따른 수소 물성치의 변화를 반드시 고려하여 계산하여야 한다. 이때 물성치 계산에 적용되는 온도는 계산 지점에서 수소의 온도와 벽면 온도의 평균값으로 한다.

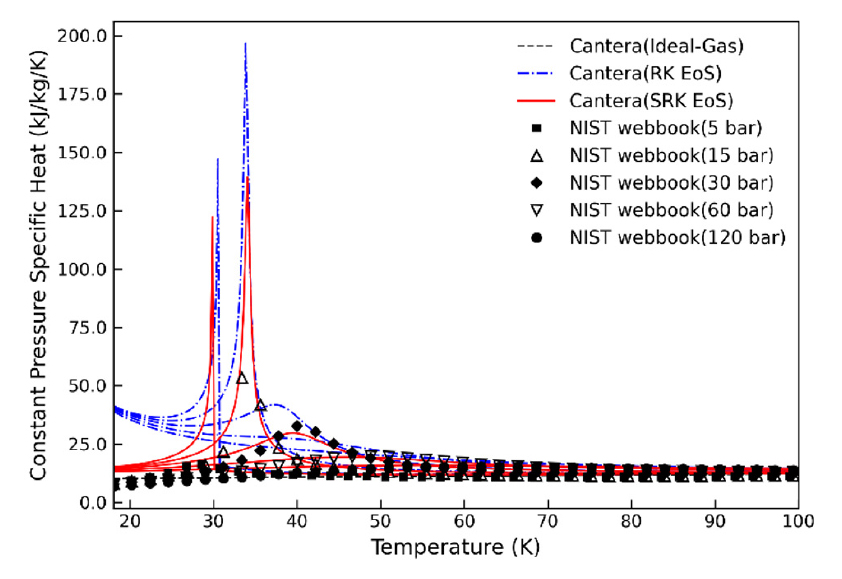
여러 가지 물질의 물성치 계산은 Chung의 EOS 식을 비롯한 다양한 모델링이 사용되고 있으며, Cantera와 같은 오픈소스 코드를 사용해도 되고, NIST 데이터를 직접 이용하여도 된다. 본 연구에서는 수소의 물성치 계산에서 비교적 정확하고 간편한 SRK(Soave-Redlich-Kwong) 상태방정식을 사용한다. 다른 모델링 및 SRK 상태방정식을 사용하여 계산한 물성치 값들에 대한 비교 데이터는 Fig. 5와 같다[16].

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F5.jpg

Fig. 5

Modelling comparision of physical properties calculation.

재생 냉각 유로의 설계는 앞서 설명한 방법으로 계산을 수행하며, 열전달 계수의 값, 노즐 및 냉각 유로의 벽면 온도, 냉각 유체의 출구 온도 등을 확인하면서 설계자가 원하는 값으로 수렴할 때까지 반복적으로 설계를 수행한다.

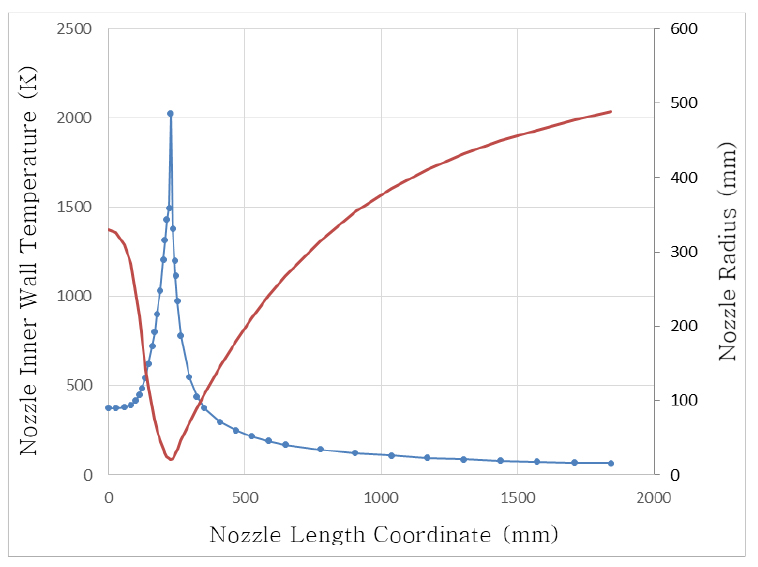
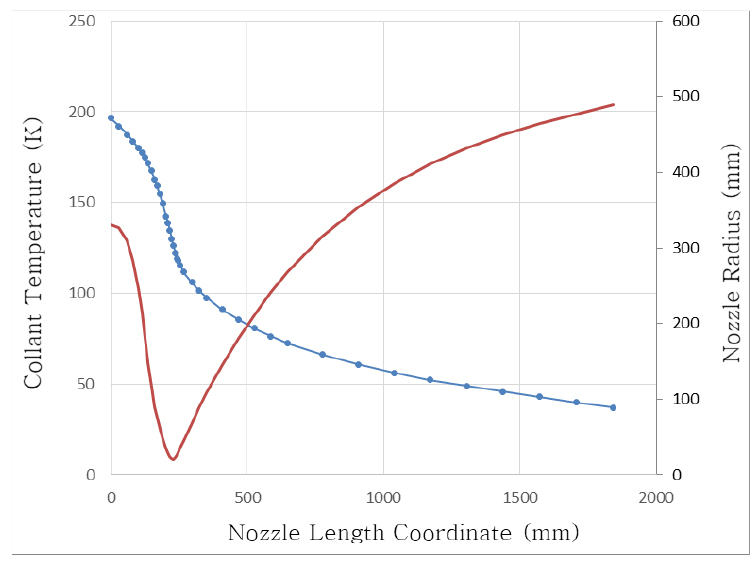
개념설계 단계에서 이러한 반복 계산을 통하여 설정된 노즐의 재생 냉각 유량은 전체 수소 추진제 양의 70%이며, 나머지 30%는 원자로의 내부 냉각에 사용한다. 냉각 계산 결과에 큰 영향을 미치는 냉각 유체의 속도는 냉각 유로의 면적에 따라 정해지며, 냉각 유로의 면적을 결정하는 유로의 높이는 3 mm로 설정한다. 그리고 벽의 두께는 1 mm, 재질은 구리합금으로 한다. 냉각 계산 결과에 큰 영향을 미치는 또 하나의 변수는 냉각 유로 내의 핀의 개수인데, 개념 설계 단계에서는 핀은 없는 것으로 하며, 추후 상세 설계가 진행되면서 최적의 핀의 개수를 정하도록 한다. 개념설계 단계에서 정해진 재생 냉각 설계 값을 바탕으로 계산된 재생 냉각 결과를 나타내면 Fig. 6와 Fig. 7과 같다.

결과에서 볼 수 있듯이 전체 추진제의 70%를 냉각 유체로 사용할 경우 노즐 내벽의 온도는 전반적으로 냉각이 잘 이루어짐을 알 수 있으나, 노즐 목 부근에서는 내벽의 온도가 1000 K 이상으로 과열되므로 향후 냉각 핀을 사용한 설계 보완이 이루어져야 될 것으로 판단된다. 계산 결과로서, 냉각 유체의 입구 온도가 37 K 이고 재생 냉각이 완료된 후의 냉각재 출구 온도는 196 K 임을 확인할 수 있으며, 재생 냉각으로 인한 냉각재의 온도 상승은 159 K 임을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F6.jpg

Fig. 6

Nozzle inner wall temperature.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F7.jpg

Fig. 7

Coolant temperature.

2.4 터보펌프 설계

우주선의 탱크에 저장된 수소를 엔진에 공급하기 위해서는 펌프가 필요하다. 저장된 수소의 압력은 2 기압이고 온도는 21 K이며 펌프의 토출 압력은 125 기압으로 설정한다. 이 때의 펌프 유량은 앞서 설명한 바와 같이 수소 추진제의 설계 유량인 1.074 kg/s 이다. 수소의 상태는 액체와 기체 사이의 초임계 상태이기 때문에 기존의 액체 펌프와는 특성이 많이 다르며 설계 시에 이에 대한 고려가 필요하다. 펌프의 구체적 사양은 향후 기본 및 상세설계 단계에서 결정하며, 시스템 해석에서 필요한 펌프 효율은 59%로 설정한다[17,18].

펌프를 구동하기 위한 터빈은 펌프와 직렬 단일 축으로 연결되며, 터빈은 설계 팽창비를 1.9로 가정하여 2단형 축류 터빈으로 구성한다. 터빈의 입구 압력, 온도 및 유량은 시스템 해석에서 결정되며, 노즐의 재생 냉각 및 핵연료의 냉각 후에 합쳐진 수소의 상태에 따라 결정된다. 터빈의 출력은 펌프를 구동하기 위한 구동력만을 필요로 하기 때문에 전체 수소 중에서 필요한 양만 터빈으로 들어간다. 펌프와 마찬가지로 시스템 해석에서 중요한 터빈의 효율은 75%로 설정한다[17,18].

3. 시스템 해석

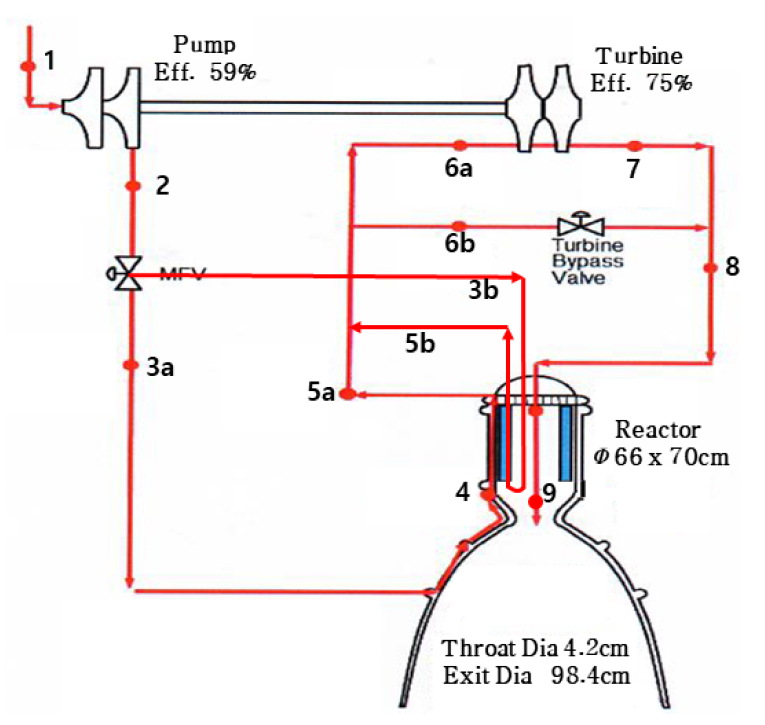
앞서 설명한 구성품들에 대한 설계값을 기준으로 시스템의 해석을 수행한다. 원자력 열추진 엔진의 구성은 앞서 설명한 바와 같이 팽창기 사이클로 구성하며 Fig. 8과 같다.

수소 탱크에서 펌프를 통하여 가압된 수소는 유량조절 밸브에서 설계 유량 1.074 kg/s의 70%는 재생냉각 입구로, 30%의 유량은 핵연료 냉각 채널로 들어간다. 냉각에 사용된 수소는 다시 합쳐져서 터빈의 입구로 흘러가며, 펌프의 구동력을 발생 시킬 수 있는 양만큼만 터빈의 입구로 들어가고 나머지 유량은 바이패스 밸브를 통과하여 터빈 출구 유량과 합쳐진다. 터빈에서 펌프의 구동력을 발생시키고 난 뒤에 압력과 온도가 낮아진 수소는 바이패스 밸브 유량과 합쳐진 뒤에 원자로 입구로 들어가서 설계 온도인 2850 K까지 상승하고 최종적으로 엔진 추력실에 모이고 노즐 목을 통과하면서 추력을 발생시킨다.

https://cdn.apub.kr/journalsite/sites/jkspe/2024-028-04/N0580280404/images/kspe_2024_284_29_F8.jpg

Fig. 8

System layout of NTP engine

3.1 “1 → 2” 구간

우주선의 탱크에서 0.22 MPa, 21 K 로 저장되어 있는 수소는 펌프를 통하여 엔진으로 유입된다. 이 때 수소는 초임계 상태이므로 온도와 압력에 따른 물성치 값의 변화가 매우 크다. 따라서 펌프 출구의 온도와 압력을 계산하기 위해서는 단순 수식으로 계산하기는 어려우며 REFPROP 데이터베이스를 사용하여 계산을 한다[19].

펌프 입구 및 출구의 상태 값과 효율의 관계를 나타내면 Eq. 12와 같다. 여기에서 탱크에 저장된 수소의 엔탈피 $h_{p_{i}}$ 는 REFPROP로 구하면 7.35 kJ/kg 이며, 등엔트로피 과정으로 설계 출구압력 12.5 MPa 까지 가압된 상태의 엔트로피 $h_{p_{o, d}}$ 는 172.8 kJ/kg 으로 구하여진다. 펌프의 효율 $η_{p}$ 은 59%로 설정하였기 때문에 펌프 출구의 엔탈피 $h_{p_{o}}$ 는 Eq. 12에 따라 287.7 kJ/kg가 된다. 펌프 출구의 압력과 엔탈피가 정해졌으므로 REFPROP로 출구 온도를 구하면 37 K이다. 그리고 설계 유량은 1.074 kg/s 이므로 펌프를 구동하기 위하여 필요한 동력은 301 kW로 계산 된다.

(12)

η_{p} = \frac{h_{p_{o, d}} - h_{p_{i}}}{h_{p_{o}} - h_{p_{i}}}

3.2 “2 → 3” 구간

펌프에서 토출된 수소는 유량조절 밸브를 지나면서 두 곳으로 나누어진다. 전체 유량의 70%인 0.752 kg/s는 노즐의 재생 냉각 입구로 보내지고, 30%인 0.322 kg/s는 핵연료 주위의 감속재와 반사체의 냉각을 위하여 원자로 내부 냉각채널로 보내진다. 이 과정에서 온도의 변화는 없는 것으로 가정하며, 압력 손실은 타 연구의 경험치를 바탕으로 3%로 설정한다[20].

3.3 “3a → 5a” 구간

앞서 재생 냉각 계산에서 설명한 바와 같이 재생 냉각 입구로 유입된 수소의 온도는 37 K이며 노즐을 냉각하고 난 뒤에 수소의 온도는 159 K 상승하여 출구 온도는 196 K가 된다. 재생 냉각 채널에서의 압력 손실은 이론적인 단순 계산은 가능하나 실제와의 오차가 크기 때문에 상세설계가 완료되기 전까지는 타 연구의 경험치를 바탕으로 가정하는 것이 바람직하다. 본 연구에서는 재생 냉각 채널에서의 압력 손실은 9%로 설정한다[20,21]. 따라서 냉각채널 출구에서의 압력과 온도는 각각 11.03 MPa, 196 K 가 된다.

재생 냉각 채널이 끝나는 지점에서 원자로의 외부 냉각이 시작된다. 원자로의 냉각은 상세설계 단계에서 다시 계산되어야 하지만 개념 설계 단계에서는 타 연구의 경험치를 바탕으로 가정하여 원자로 열용량의 1% 정도가 원자로의 외부로 방출되는 것으로 가정한다. 그리고 이 구간에서의 압력 손실은 5%로 가정한다[20,21]. 따라서 원자로의 외부 냉각이 끝나는 지점에서의 압력과 온도는 각각 10.48 MPa, 238 K가 된다.

3.4 “3b → 5b” 구간

펌프에서 토출된 수소의 30%인 0.322 kg/s는 원자로의 내부 냉각 채널로 보내지는데, 이때의 압력과 온도는 각각 12.13 MPa, 37 K이다. 원자로의 내부 냉각 채널은 매우 복잡하게 설계되며, 감속재와 반사체를 적정한 온도 이하로 유지할 수 있도록 해야 한다. 따라서 방출 열량과 압력 손실은 개념설계 단계에서는 예측하기가 어렵기 때문에 타 연구의 경험치를 바탕으로 가정한다[20,21,22]. 원자로의 내부 냉각으로 방출되는 열량은 원자로 열용량의 8%로 가정하였으며, 따라서 감속재와 반사체를 냉각시키고 난 뒤의 냉각재 온도는 857 K가 된다.

3.5 “6 → 7 → 8” 구간

노즐의 재생 냉각을 거쳐 원자로의 외부 냉각에 사용된 수소와 원자로의 내부 냉각에 사용된 수소는 합쳐져서 터빈의 입구로 들어간다. 이때의 수소의 압력과 온도는 각각 10.48 MPa, 424 K이다. 터빈으로 들어가는 수소는 수소 펌프를 작동시키기 위한 동력을 발생시키는데, 펌프와 터빈의 동력이 평형을 이루도록 터빈의 유량을 조절하여 필요한 양만 터빈으로 들어가고 나머지는 바이패스 시킨다.

터빈의 효율 및 터빈에서 만들어진 동력을 수식으로 나타내면 Eq. 13과 Eq. 14와 같다. 펌프에서와 같이 터빈 전후로도 물성치의 변화가 크기 때문에 REFPROP 데이터베이스를 사용하여 계산한다. 터빈 입구의 엔탈피 $h_{t_{i}}$ 는 5818 kJ/kg이고, 터빈의 팽창비는 1.9로 가정하였으므로 등엔트로피 과정을 거쳐서 출구압력 5.52 MPa인 상태의 엔탈피 $h_{t_{o, d}}$ 는 4753 kJ/kg이다. 터빈의 효율 $η_{t}$ 은 75%로 가정하였으므로 터빈 출구의 엔탈피 $h_{t_{o}}$ 는 Eq. 13에 따라 5020 kJ/kg으로 계산된다. 따라서 수소 펌프와 축 동력의 평형을 이루기 위하여 필요한 터빈의 입구 유량은 Eq. 14에 따라 0.385 kg/s로 계산된다. 이때 펌프와 터빈을 연결한 축의 기계적 손실은 2%로 가정한다. 터빈 출구의 엔탈피와 압력으로부터 구하여진 터빈 출구의 온도는 371 K이다.

(13)

η_{t} = \frac{h_{t_{i}} - h_{t_{o}}}{h_{t_{i}} - h_{t_{o, d}}}

(14)

W_{t} = {\dot{m}}_{t} (h_{t_{i}} - h_{t_{o}})

3.6 “8 → 9” 구간

터빈 출구의 수소와 터빈으로 들어가지 않고 입구에서 바이패스된 수소가 합쳐져서 원자로의 핵연료로 들어간다. 이때 수소의 압력과 온도는 각각 5.52 MPa, 406 K이다. 핵연료로 유입되고 난 뒤에 수소의 온도는 상승되고, 압력은 떨어져서 엔진 추력실에 모여지게 된다. 원자력 열추진 엔진의 요구 성능인 추력 10 kN 및 비추력 950초를 만족하기 위해서는 앞서 노즐형상 설계시에 설명한 바와 같이, 엔진 추력실의 온도와 압력이 설계 조건인 온도 2850 K 및 압력 4.41 MPa로 형성되어야 한다. 따라서 수소의 온도를 높이기 위한 핵연료의 열용량은 49.3 MW가 되어야 하며, 압력손실은 20% 이하가 되어야 한다. 또한 수소 가열을 위한 열용량과 외부 및 내부 냉각으로 방출된 열용량을 모두 고려하면 핵연료의 총 열용량은 53.7 MW로 설계되어야 한다.

4. 시스템 해석 결과

추력 10 kN 및 비추력 950초를 만족하는 원자력 열추진 엔진의 개념설계를 바탕으로 시스템 해석을 수행하였다. 엔진의 성능 요구 사양을 만족하기 위한 수소의 유량은 1.074 kg/s이며, 엔진 추력실의 정체 조건은 온도 2850 K, 압력 4.41 MPa이다. 이 같은 엔진 추력실의 조건을 형성하기 위해서는 301 kW 동력의 수소펌프가 필요하며, 원자로 핵연료의 열용량도 53.7 MW가 되어야 한다.

시스템의 해석 결과는 시스템을 구성하는 각 부품의 성능에 따라 크게 달라진다. 수소 펌프의 효율과 수두, 수소 터빈의 효율과 팽창비, 각 밸브 및 배관의 압력 손실 등이 해석 결과에 크게 영향을 미치기 때문에 설계가 진행되면서 반복적인 계산으로 수정되어야 한다. 특히 노즐의 재생냉각 계산 및 원자로의 외부와 내부의 냉각 계산은 상세한 수치적 계산 및 실험을 통하여 정확한 결과가 시스템의 해석으로 계속 피드백되어야 할 것이다. 개념설계 단계에서 최종 확정된 시스템의 해석 결과는 Table 1과 같다.

Table 1

Results of system analysis.

Point	P (MPa)	T (K)	$\dot{m}$ (kg/s)
1	0.22	21	1.074
2	12.50	37	1.074
3a	12.13	37	0.752
3b	12.13	37	0.752
4	11.03	196	0.752
5a	10.48	238	0.752
5b	10.48	857	0.322
6a	10.48	424	0.385
6b	10.48	424	0.689
7	5.52	371	0.385
8	5.52	406	1.074
9	4.41	2850	1.074

5. 결 론

추력 10 kN 및 비추력 950초의 성능 만족하는 원자력 열추진 엔진의 개념설계 및 시스템 해석을 수행하였다. 개념설계는 핵연료를 포함한 원자로, 수소 펌프 및 수소 터빈에 대하여 수행되었으며, 노즐의 형상 설계 및 노즐의 재생 냉각 설계 및 해석이 수행되었다. 또한 개념 설계를 바탕으로 수소 탱크에서부터 엔진 추력실에 이르는 전체 시스템에 대한 해석이 수행되었다.

원자력 열추진 시스템에 대한 개념설계 및 시스템 해석을 통하여 화성 탐사용 우주선의 추진 기관으로 사용 가능한 새로운 개념의 엔진이 현재의 기술로 충분히 개발 가능하다는 것을 확인하였다. 또한 기본 및 상세설계 단계로 설계가 성숙되어 가면서 계속적인 수정이 필요하지만, 원자력 열추진 엔진의 개발 목표를 설정하기 위하여 수행된 개념 설계 결과가 적정함을 시스템 해석을 통하여 확인하였다.

References

Robbins, W.H. and Finger, H.B., "An Historical Perspective of the NERVA Nuclear Rocket Engine Technology Program," NASA CR 187154, 1991.

10.2514/6.1991-3451

Proust, E., "Lecture Series on Nuclear Space Power & Propulsion Systems - Nuclear Thermal Propulsion Systems," hal-03147500, 2021.

Wetch, J.R., Goldin, A.Y., Koroteev, A.A., Konopatov, A.D., Pavshook, V.A., Ponomarev-Stepnoy, N.N., Semyonov, V.F. and Fedik, I., "Development of Nuclear Rocket Engines in the USSR," AIAA/ NASA/OAI Conference on Advanced SEI Technologies, 1991.

Powell, J., Maise, G., Ludewig, H. and Todosow, M., "High Performance Ultra-light Nuclear Rockets for NEO (Near Earth Objects) Interaction Missions," BNL 63581, 1996.

Ludewig, H., Powell, J.R., Todosow, M., Maise, G., Barletta, R. and Schweitzer, D.G., "Design of Particle Bed Reactor for the Space Nuclear Thermal Propulsion Program," Progress in Nuclear Energy, Vol 30, No. 1, pp. 1-65, 1996.

10.1016/0149-1970(95)00080-4

Powell, J.R., Ludewig, H. and Todosow, M., "Summary of Particle Bed Reactor Design for the Space Nuclear Thermal Propulsion Program," NASA STI/Recon Technical Report N, 94, 32266.

Paniagua, J.C., Powell, J.R. and Maise, G., "Design and Development of the MITEE-B Bi-Modal Nuclear Propulsion Engine," AIP Conference Proceedings, Vol. 654, No. 1, pp. 438-444, 2003.

10.1063/1.1541323

Borowski, S.K., McCurdy, D.R. and Packard, T.W., "Nuclear Thermal Rocket/Vehicle Characteristics and Sensitivity Trades for NASA's Mars Design Reference Architecture (DRA) 5.0 Study," 2009 Nuclear and Emerging Technologies for Space, Atlanta, GA, 2009.

10.2514/6.2009-5308

Drake, B.G., Hoffman, S.J. and Beaty, D.W., "Human Exploration of Mars Design Reference Architecure 5.0," IEEE Aerospace Conference, pp. 1-24, IEEE, 2010.

10.1109/AERO.2010.544673620095027

Houts, M.G., Kim, T., Emrich, W.J., Hickman, R.R., Broadway, J., Gerrish, H.P., Glenn, D., Belvin, A., Borowski, S.K. and Scott, J. "The Nuclear Cryogenic Propulsion Stage," 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, U.S.A., AIAA 2014-3724, 2014.

10.2514/6.2014-3724

Emrich, W.J., "Promises and Challenges of Nuclear Propulsion for Space Travel," IAEA Webinar, 2022.

Borowski, S.K., McCurdy, D.R. and Packard, T.W., "Nuclear Thermal Propulsion (NTP): A Proven Growth Technology for Human NEO/Mars Exploration Missions," IEEE Aerospace Conference, pp. 1-20, IEEE, 2012.

10.1109/AERO.2012.6187301PMC3420957

Yang, S.S. and Cho, N., "Conceptual Research on Nuclear Propulsion System for Deep Space Exploration," KARI Report, 2023.

Hong, Y.S., "Space Propulsion Engineering," Chnugmoongag Publishing, Seoul, 1998.

Binder, M., Tomsik, T. and Veres, J.P., "RL10A-3-3A Rocket Engine Modeling Project," NASA TM 107318, 1997.

Kang, S.Y., Kim, S.K., Ryu, C. and Moon, I., "Development of Design Code for Oxidizer-Rich Preburner of Staged Combustion Cycle Engine Using Cantera," Journal of the Korean Society of Propulsion Engineers, Vol. 26, No. 6, pp. 10-20, 2022.

10.6108/KSPE.2022.26.6.010

Leto, A., Votta, R. and Bonfiglioli, A., "Preliminary Design Method of a Turbopump Feed System for Liquid Rocket Engine Expander Cycle," Energy Procedia, Vol. 101, pp. 614-621, 2016.

10.1016/j.egypro.2016.11.078

Chen, S.C.S., Veres, J.P. and Fittje, J.E., "Turbopump Design and Analysis Approach for Nuclear Thermal Rockets," AIP Conference Proceedings, Vol. 813, No. 1, pp. 522-530, American Institute of Physics, 2006.

10.1063/1.2169230

Lemmon, E.W., Bell, I.H., Huber, M.L. and McLinden, M.O., NIST Standrad Reference Database 23: Reference Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology, Standard Reference Data Program, Gaithersburg, 2018.

Belair, M.L., Sarmiento, C. and Lavelle, T., "Nuclear Thermal Rocket Simulation in NPSS," NASA TM 2013-216553, 2013.

10.2514/6.2013-4001

Nikitaeva, D. and Thomas, D.L., "Alterative Propellant Nuclear Thermal Propulsion Engine Architectures," Journal of Spacecraft and Rockets, Vol. 59, No. 4, pp. 1149-1160, 2022.

10.2514/1.A35289

Nam, S.H., Venneri, P., Kim, Y., Lee, J.I., Chang, S.H. and Jeong, Y.H., "Innovative Concept for an Ultra-small Nuclear Thermal Rocket Utilizing a New Moderated Reactor," Nuclear Engineering and Technology, Vol. 47, No. 6, pp. 678-699, 2015.

10.1016/j.net.2015.06.003

Journal of the Korean Society of Propulsion Engineers ISSN:1226-6027(Print) 2288-4548(Online) 한국추진공학회지

Preview

Conceptual Design and System Analysis of 10 kN Nuclear Thermal Propulsion Engine

ABSTRACT

MAIN

Fig. 1

Nuclear thermal engine cycles.

Fig. 2

Specific impulse depending on nuclear fuel.

Fig. 3

Nuclear reactor and fuel.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Fig. 4

Layout of engine nozzle.

(9)

(10)

(11)

Fig. 5

Modelling comparision of physical properties calculation.

Fig. 6

Nozzle inner wall temperature.

Fig. 7

Coolant temperature.

Fig. 8

System layout of NTP engine

(12)

(13)

(14)

Table 1

Results of system analysis.

References