1. 서 론
2. 해석 기법 모델링
2.1 특성곡선법을 이용한 M&S
2.2 AMESim을 이용한 M&S
3. 해석 기법의 검증
3.1 조건 A
3.2 조건 B
4. M&S 기법의 성능 분석
4.1 정확도
4.2 계산 소요 시간
5. 결 론
Nomenclature
ρ : denstity
SG : specific gravity
g : gravitational acceleration
c : wave speed
D : diameter
A : area
H : head
V : velocity
Q : flow rate
ks : steady friction factor
ku : unsteady friction factor
CV : valve flow coefficient
R : rotating rate of valve
1. 서 론
비행체의 추진기관을 구성하는 주요소 중 하나인 추진제 공급 시스템(이하, 공급 시스템)은 엔진이 안정적으로 운용될 수 있도록 추진제를 공급하는 역할을 한다. 공급 시스템은 독립적인 기능을 수행하는 하위 구성품들의 상호작용을 통해 하나의 시스템 단위로 작동하므로, 각 부품의 제원 및 시스템의 전반적인 구성에 의해 엔진의 효율, 안정성과 같은 성능이 크게 변화할 수 있다. 안정성의 측면에서 공급 시스템의 이상은 엔진의 오작동을 야기할 수 있으며 이는 발사 임무 실패의 주원인이 될 수 있다[1]. 특히 엔진의 시동 및 정지, 혹은 단분리 등의 이벤트 시점에서는 요구되는 추진제의 공급을 위해 고속의 밸브 개폐가 이루어질 수 있다. 이때 관내 유체의 운동에너지가 압력으로 변환되며 급격한 압력 상승이 발생할 수 있다. 이로 인해 구성품의 일부가 손상되어 그 기능을 상실할 경우, 엔진의 파손으로 이어질 수 있다. 또한 해당 과정에서 발생한 압력파는 관을 따라 이동하며 진동을 유발하는데 이는 시스템의 불안정성을 야기한다. 그 예시로 소련의 N1-L3 로켓은 단분리 단계 시 이루어지는 밸브의 급격한 폐쇄로 인해 펌프가 손상되어 임무에 실패했다[2]. 이러한 이유로 엔진이 안정적으로 운용될 수 있도록 공급 시스템을 적절히 설계하는 것이 중요하며, 이에 기반이 되는 데이터를 확보하는 것이 필요하다. 다양한 운용 조건에서의 데이터를 보유하면 효율적인 시스템 설계가 가능하고 엔진의 운용 과정에서 발생 가능한 문제를 사전에 방지하는 것이 가능하다.
일반적으로 시스템의 설계와 운용 조건에 따른 데이터의 확보는 M&S(Modeling&Simulation)를 통해 이루어진다. M&S는 시스템의 물리적 특성을 적절히 모사한 모델링을 바탕으로 시뮬레이션을 수행하는 절차로, 특히 초기에 시스템을 개발할 때, 그 결과를 설계에 반영하고 다시 해석하는 반복적인 과정에서 활용된다. 따라서 시간 및 비용과 같은 자원이 한정된 환경에서, 활용하고자 하는 M&S의 성능이 전반적인 개발 효율에 영향을 미칠 수 있으므로 이에 대해 파악하고 평가하는 것이 필요하다[3,4].
보편적으로 공급 시스템의 M&S에는 OOMS(Object – Oriented Modeling and Simulation) 프로그램이 사용되어 왔다. Multi – domain 모델링에 특화된 OOMS 프로그램은 다양한 분야의 물리적 모델을 결합하여 시뮬레이션하기 용이하다는 장점이 있으며, 물리적 모델링이 적용되어 모듈화된 구성 요소를 연결하는 방식을 취하므로 편리하게 사용할 수 있다. 주로 DAE(Differenctial Algebraic Equation)/ODE(Ordinary Differential Equation) 솔버 혹은 PDE(Partial Differential Equation) 솔버를 선택하여 해석을 수행한다. EcosimPro와 AMESim이 대표적인 프로그램으로, 이를 통해 시동 과정과 같이 특정 시퀀스에서의 추진제 공급 특성을 확인하는 연구가 수행되었다. EcosimPro 기반에서 구현된 ESA의 ESPSS를 통해 RL10A-3-3A 엔진의 시동 과정을 해석한 사례[5]가 있으며, SpaceLiner의 동특성에 관한 해석도 진행된 바 있다[6]. 인공위성의 priming 과정에서 발생하는 워터 해머 현상에 대한 해석도 이를 통해 수행되었다[7]. 상용프로그램인 AMEsim을 이용한 시뮬레이션을 통해 Crossfeed 시스템에서의 유동 특성을 확인한 연구 사례 역시 존재한다[8]. 국내에서는 손민 등[9]이 70톤급 엔진을 설계하고 시동 과정을 해석하였다. 한편, 추진 기관의 공급 시스템뿐만 아니라 유압 분야에서도 공급과 관련된 M&S가 진행된 바 있다. 모듈화된 모델을 사용한 앞선 사례들과는 달리, 파이프 내부 유동을 계산하는 것에 용이한 특성곡선법을 주로 활용하여 대형 상하수도 혹은 플랜트의 시스템을 해석하였다[10,11,12,13,14]. 이와 관련하여 Pérez와 Dormido는 DAE에 기반한 프로그램과 MOC를 활용하여 단순한 요소로 구성된 상하수도 시스템에 대해 각각 시뮬레이션을 수행하고 계산 성능을 비교하였다[14]. 결과적으로 이러한 해석 기법을 통해 빠른 계산 시간을 확보할 수 있다는 장점을 확인하였으나, 해석의 대상이 되는 시스템이 엔진과는 상이하였으며, 이외에도 추진 기관의 공급 시스템에 중점을 두고 M&S 방법의 성능을 평가한 연구는 보고된 바가 거의 없다.
이에 본 연구에서는 특성곡선법 코드와 AMESim, 두 가지의 M&S 해석 기법을 적용하여 액체 추진제를 사용하는 일반적인 공급 시스템을 해석하고 결과를 비교함으로써 각각의 성능을 평가하고자 하였다. 기 수행된 사례[14]와 유사하나 구성은 보다 복잡한 형태의 엔진의 공급 시스템에 대해 특성곡선법과 상용프로그램을 이용하여 각각 M&S를 수행하였다. 또한 수류 시험 장치를 이용한 실험을 통해 해석 결과의 타당성을 검증하고 최종적으로는 이를 바탕으로 정확도와 시뮬레이션 성능을 비교하여 각 M&S 기법에 대해 평가하고자 하였다.
2. 해석 기법 모델링
본 장에서는 엔진의 공급 시스템을 구성하는 대표적인 요소들을 선정하여 모델링하고 해석하는 방법에 대해 서술하고자 한다. 특정 요소의 변화에 의한 외란의 전파를 나타내는 특성곡선법을 적용한 모델링과 OOMS 기반 상용 프로그램인 AMESim을 이용한 모델링, 두 가지 방법을 간략히 소개하고자 한다.
2.1 특성곡선법을 이용한 M&S
기본적으로 공급 시스템의 각 구성품을 연결하여 추진제가 흐를 수 있도록 하는 파이프의 계산 식에 타 요소들의 모델링 식을 경계조건으로 적용하여 해석을 수행하였다. 파이프는 압축성과 관성 효과를 고려하여 Eq. 1의 연속방정식과 Eq. 2의 운동방정식으로 표현하였다. Eq. 2의 ks와 ku는 관 내 유동 마찰 손실 계수로 정적 상태에서는 Haaland 식[15]을, 동적 상태에서는 Brunone 식[16]을 통해 계산된다.
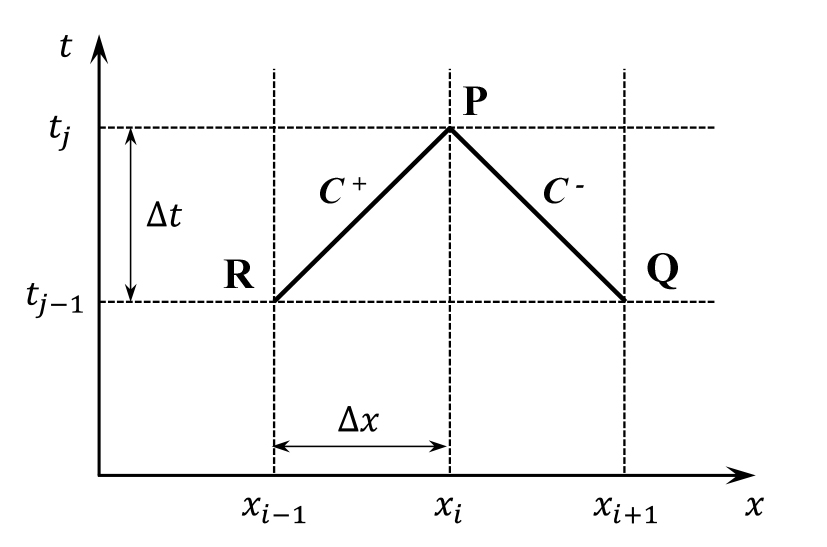
매개변수와 특성곡선 조건인 을 이용하여 편미분 방정식 형태의 Eq. 1-2를 정리하면 Eq. 3과 같이 t에 대한 두 개의 상미분 방정식으로 표현할 수 있다. 기존에 두 개의 독립 변수 x, t로 표현된 편미분 방정식과 달리 t 하나에 대한 미분 방정식으로 표현되어, 특성곡선을 따라 특정 시점 t에서의 V와 H가 결정된다. 이를 Fig. 1의 점들을 통해 유한차분 형태로 표현하여, 구하고자 하는 미지수에 대한 식으로 정리하면 최종적으로 Eg. 4와 같이 나타낼 수 있다. 여기서 Fig. 1의 P점을 구하고자 하는 점으로 정의하면, 해당 지점에서의 V와 H는 각각 VP와 HP로 표현된다. 또한 Eq. 4의 CR과 CQ는 계산 대상 지점인 P점 이전에 계산된 R, Q점에서의 정보를 정리한 항이며, Ca는 중력가속도, 압력파 속도, 마찰 계수 등에 의해 결정되는 값이다[17]. 따라서 미지수 VP와 HP를 제외한 모든 값을 알고 있으므로 연립 방정식을 풀어 두 값을 계산할 수 있다.
파이프로 연결되는 공급 시스템의 타 구성 요소는 탱크, 펌프, 밸브로, 각 요소에 의해 발생하는 물리적 현상을 경계조건으로 적절히 적용하여 모사해야 한다. Table 1에 모든 구성품들에 대해 유속()과 압력의 관계를 수식으로 모델링한 결과를 제시하였다. 추진제를 저장하는 탱크의 경우, 출구로 토출되는 유동의 속도로 시간에 따른 레벨 변화를 표현하였다. 펌프와 밸브는 각 성능에 의해 결정되는 계수를 활용하여 모델링하였다. 펌프의 경우, 일정한 회전 속도에서 펌프에 의해 가압되는 양을 유량에 대한 이차식 형태로 나타내는 성능곡선으로 표현하였다. 또한 밸브는 유량 계수를 통한 수식으로 유량과 전후단의 차압 관계를 나타냈다. Table 1의 모델링 식들은 구성품이 위치한 곳에서 경계조건으로 적용되어 Eq. 3과 연립함으로써 값이 도출된다.
2.2 AMESim을 이용한 M&S
M&S 해석 기법의 비교를 위해 SIEMENS社의 멀티 도메인(multi domain) 모델링 환경 범용 해석 프로그램인 AMESim을 이용하여 해석을 수행하였다. 기본적으로 유체의 공급 과정을 해석하는 것이므로 AMESim의 여러 라이브러리 중 hydraulic, hydraulic resistance의 모델을 주로 활용하여 시스템을 구현하였다. 이외에도 펌프와 밸브를 모사하기 위한 모델을 추가하여 다음 장에서 서술할 실험과 같은 조건으로 구동하도록 하였다.
실험에서는 상온의 물을 작동 유체로 사용하였으므로 해석에서도 이와 동일하게 적용하였다. 유체의 물성치는 프로그램에 내장된 테이블을 활용하였다. 유체가 저장되는 탱크의 경우, 초기 수위와 단면적, 가압량을 초기값으로 입력하면 시간에 따른 토출 압력이 계산되는 모델을 통해 표현하였다. 펌프는 일정한 회전수를 입력받아 성능곡선에 따라 전후단의 압력과 유량이 계산된다. 밸브는 구동 방식에 따라 유량 계수를 고정하거나, 시간에 따라 유량 계수가 변하도록 가변 신호를 입력할 수 있도록 하여 구현하였다. 파이프는 연속방정식과 1D 운동방정식을 기반으로 표현된 모델을 사용하였다. 두 식은 모델 내에 내장된 PDE 솔버인 Two step – Lax Wendroff 방법을 통해 계산된다. AMESim에서는 Haaland 모델과 Zielke 모델을 활용하여 마찰 계수를 도출하여, 최종적으로 유체의 점성에 의한 마찰 손실을 계산한다. 앞선 모델링과 동일하게 정적 상태에서는 Haaland 식이 활용되었으며, 동적 상태에서는 Zielke 식이 적용되었다[18]. 동적 마찰계수를 예측하기 위한 식은 다양하지만, Brunone와 Zielke, 두 식 모두 선행 연구들을 통해 충분히 검증되었다[16,19].
모든 해석에서 두 기법을 활용한 M&S는 동일한 조건 및 계산 환경에서 수행되었다. 해석을 위해 사용된 컴퓨터의 제원은 Table 2에 정리되어 있다. 또한 해석 결과는 실험에서의 계측 지점과 동일한 위치에서 압력과 유량을 출력하여 확인하였다.
3. 해석 기법의 검증
수행한 M&S 결과를 검증하기 위해 수류 시험 장치를 이용하여 실험을 수행하였다. 검증을 위한 적절한 조건을 설정하여 실험을 수행한 후, 이를 바탕으로 M&S의 타당성을 확인하였다. 실험 장치와 동일한 제원 및 실험 조건을 모델링 과정에 반영하여 해석을 수행하였다.
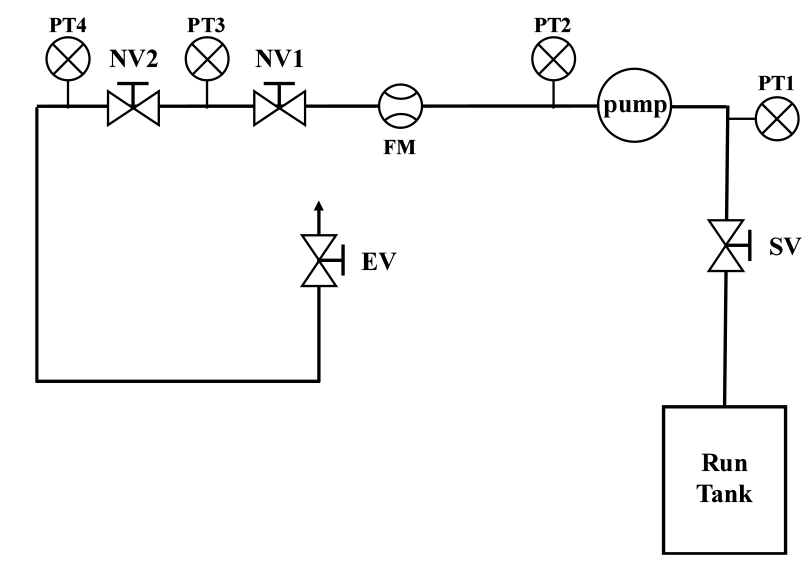
Fig. 2는 수류 시험 장치의 구성을 나타낸다. 실험 장치는 개방형으로 구축되어 있어, 공급 탱크에서 시작된 유동은 3/4 ʺ 스테인레스 튜브 공급관을 따라 흘러 최후단의 회수 탱크에서 회수된다. 유체의 공급과 중단은 공급 탱크와 관을 연결해주는 솔레노이드 밸브(SV)를 통해 제어되며, 유체의 가압은 솔레노이드 밸브의 후단에 설치된 펌프를 통해 이루어진다. 펌프의 경우, SPECK社의 ‘CY-4281-MK’ 모델로, 전후단의 압력 센서를 통해 가압량을 확인할 수 있다. 펌프 이후에는 유량 제어 및 차압 모사를 목적으로 니들 밸브가 총 2개(NV1, NV2) 설치된다. 이 중 두 번째에 위치한 밸브에서 유량이 조절되며 모터를 통해 밸브의 구동이 이루어진다. NV2의 원활한 구동을 위해 밸브의 토크를 고려하여 모터와 기어를 함께 활용하여 구동하였다. 또한 장치의 최후단에 밸브(EV)가 설치되어, 관의 종점과 회수 탱크를 연결한다. EV는 신텍코리아의 ‘STS22C’ 시리즈의 모델을 사용하였다. 전력 공급과 중단을 통해 밸브가 구동되며 전원이 인가되면 최대 0.08 초의 반응 속도로 밸브가 개방되고 전원 공급이 중단되는 경우에는 최대 0.1 초의 반응 속도로 폐쇄된다.
수류 시험 장치에는 총 5개의 센서가 설치되며, 그 중 4개는 압력을, 1개는 유량을 계측한다.
Fig. 3은 센서들을 포함한 구성품의 위치를 나타낸다. 구성품의 전후단에서 압력(PT1~PT4)을 측정하여 차압을 확인할 수 있도록 하였으며, 펌프 후단에는 유량계(FM)를 설치하여 관에 흐르는 유량을 계측할 수 있도록 하였다.
실험은 동적 마찰 계수가 지배적인 정도를 기준으로 하여 다음 두 가지 조건에 대해 수행하였다. 일반적으로 유량의 변화율이 크지 않은 경우에는 동적 마찰 계수에 대한 영향이 거의 없는 반면, 유량의 변화율이 큰 경우에는 동적 마찰 계수에 의한 영향이 지배적으로 작용한다. 동적 마찰 계수의 경우, 예측이 다소 어려우며 다양한 모델이 존재하므로 이에 대한 검증이 이루어져야 한다. 따라서 두 조건에 대해 실험과 해석을 수행하고 이를 비교함으로써 검증하고자 하였다.
3.1 조건 A
실험이 진행되는 동안 NV2가 구동되어 유량이 변화되는 조건을 선정하였다. 해당 조건에서는 비교적 느린 구동을 수행하여 유량의 변화율 크지 않도록 하였다.
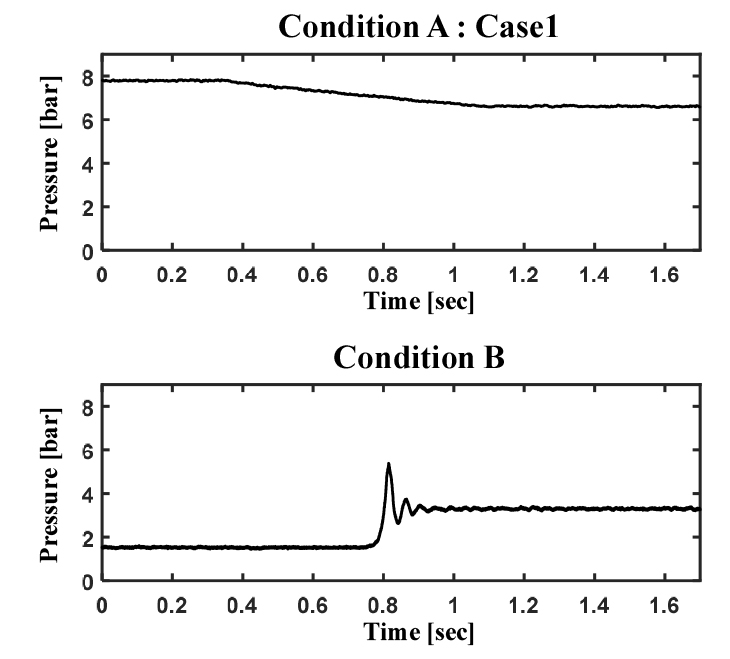
본 실험에서는 NV2를 한 바퀴 회전시켰을 때를 R=1로 정의하고 초기 NV2 개도율을 Rstart로 나타내었다. 실험 초기에 NV2를 각 조건에 해당하는 Rstart로 설정한 후, 정상 상태 흐름이 형성되면, Δt=0.75 초 동안 모터를 구동하여 NV2를 개방한다. 두 실험 케이스 모두 Rstart를 제외한 조건은 동일하다. 또한 NV2를 제외한 다른 구성품들은 실험 시간 동안 변화하지 않도록 하였다. 즉, NV1은 완전 개방하여 고정하였고 펌프는 일정 회전수를 유지하도록 하였다. 각 실험 케이스에 해당하는 조건은 Table 3에 정리하였다. Fig. 4의 상단 그래프와 같이 해당 조건의 실험을 통해 밸브 구동을 따라 압력이 서서히 상승하는 것을 확인할 수 있다.
Table 3
Test conditions of Condition A.
| Test case | Case1 | Case2 | |
| NV1 | Full open | ||
| NV2 | Rstart | 0.25 | 0.75 |
| ΔR | 0.25 | ||
| Δt | 0.75 s | ||
| Pump | 3,400 rpm | ||
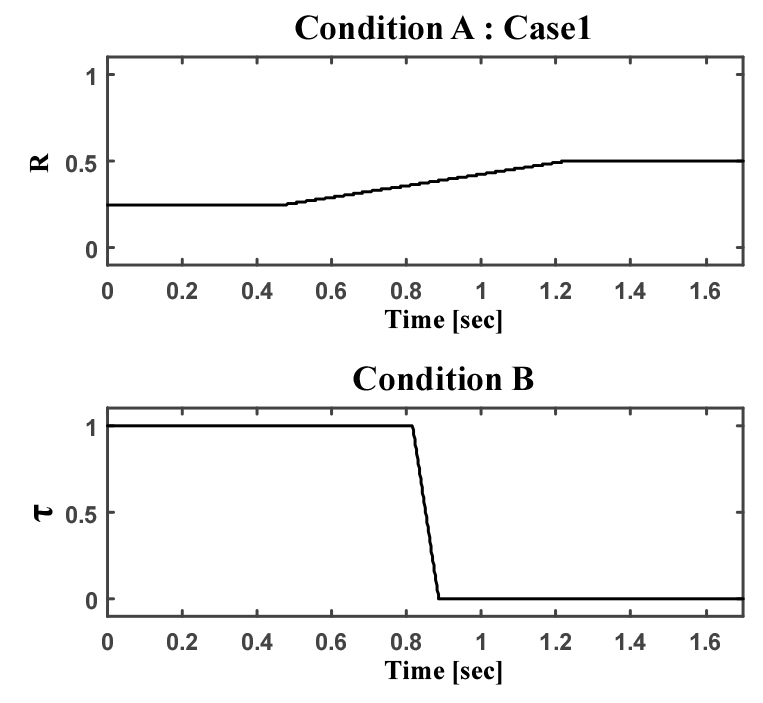
위의 실험과 동일한 조건으로 해석을 함께 수행하였으며, 실험을 통해 측정된 압력과 유량을 통해 Table 1의 밸브의 유량 계수와 펌프의 상수를 도출하여 이를 반영하였다. 또한 밸브가 구동되는 것을 해석에 적용하기 위해 개도율이 변화하여 유량 계수가 변경되도록 하였다. 실험과 동일하게 총 변화 시간은 0.75 초로 하였으며 이는 Fig. 5의 상단 그래프에 나타냈다. 조건 A의 두 케이스는 초기 개도율을 제외한 변화율이 동일하므로 Case1에 대한 데이터를 대표로 나타내었다.
3.2 조건 B
다음으로는 동적 마찰 계수가 지배적인 조건에 대한 실험을 수행하였다. 이를 위해 장치 최후단에 위치한 밸브(EV)를 구동하였다. 실험 초기에는 전원을 인가하여 EV를 완전히 개방해 유체가 흐르도록 한 후, 일정 시간이 지나 유동이 정상 상태에 도달하면 전원 공급을 중단시켜 밸브를 폐쇄한다. 정상 상태의 흐름을 유지하던 유동은 밸브의 급격한 폐쇄로 인해 운동에너지가 모두 압력에너지로 변환되어 압력 상승이 발생한다. 상승한 압력은 Fig. 4의 하단 그래프와 같이 몇 번의 진동을 거치며 감쇠되어 정상 상태에 도달한다. 이는 앞선 조건 A와는 달리 비정상 특성이 강하게 나타나는 조건으로, 동적 마찰 계수에 의한 영향을 크게 받는다. 따라서 해당 조건에서의 실험과 해석 결과를 비교함으로써 검증을 수행하고자 하였다.
Table 4에 정리된 바와 같이, 실험 시간 동안 NV1과 NV2는 완전 개방된 상태로 고정되고 펌프의 회전수는 조건 A보다 낮은 1,780 rpm으로 유지된다. 큰 압력 상승으로 인한 펌프의 손상이 우려되어, 낮은 rpm으로 펌프를 구동하였다. EV의 경우, 유량이 0.1초 내에 초기값에서 0으로 감소하여 공급이 완전히 중단될 수 있도록 구동하였다. 실험을 통해 압력이 0.1초 내에 상승하는 것을 확인하여, 해당 시간 내에 밸브의 구동이 이루어졌다고 판단할 수 있다. 실험 결과를 통해 확인한 시간을 Fig. 5의 하단의 그래프와 같이 해석에 반영하였다. τ는 무차원화된 밸브의 개방 정도로, 1은 완전히 개방된 상태를, 0은 완전히 폐쇄된 상태를 의미한다.
4. M&S 기법의 성능 분석
각 실험 조건에 대해 특성곡선법을 적용한 코드와 AMESim, 두 가지 M&S 해석 결과를 실험과 비교하여 검증을 수행하고 정확도와 계산 시간 측면에서 두 방법을 비교하였다.
4.1 정확도
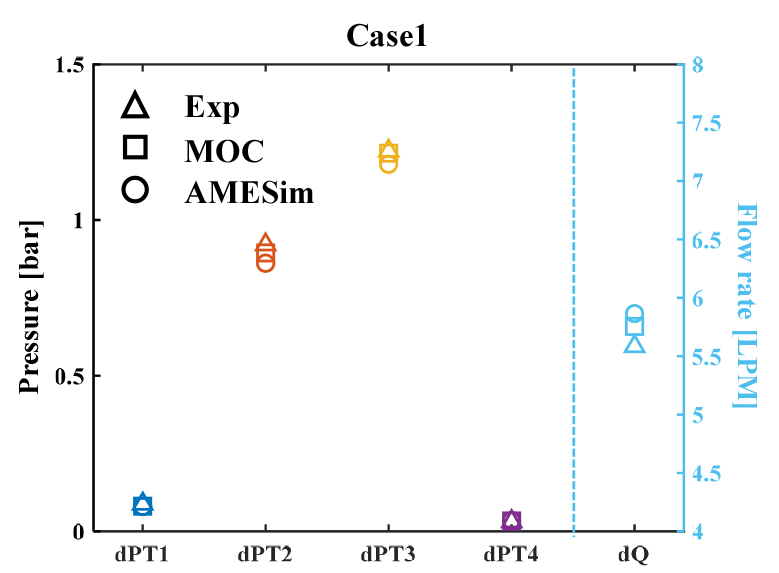
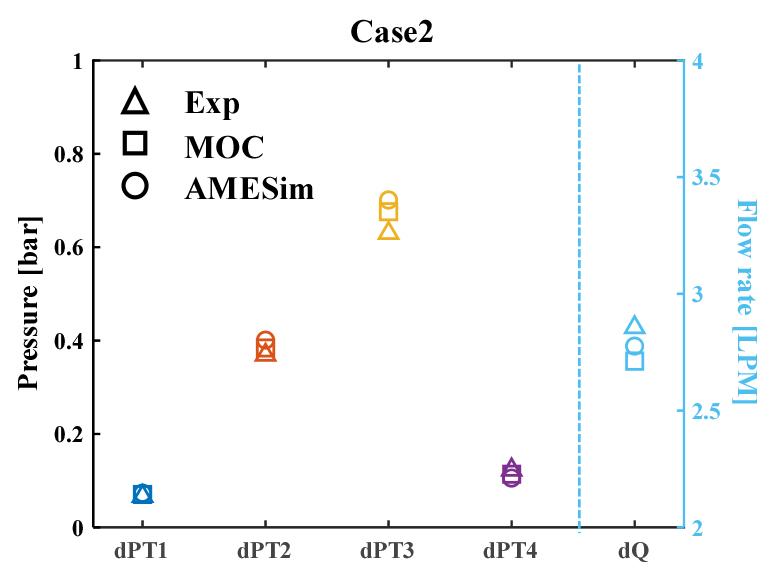
Fig. 7,8,9은 실험과 두 M&S 결과를 비교한 결과이다. Fig. 5와 같이 실험 시, 일정 시간 동안 밸브가 구동되므로 시간이 지남에 따라 압력과 유량이 변화한다. 따라서 실험을 통해 구동 시간과 시점을 알 수 있으므로 구동 전후의 압력 차(dP)와 유량 차(dQ)를 계산하여 그 값을 비교하였다. 모든 케이스의 결과는 Fig. 3에 표시된 위치에서의 값을 통해 제시하였다. 조건 B의 유량의 경우, 실험 장치에 설치된 유량계의 반응 속도 제한으로 인해 해석 결과와 비교가 어려워, 해당 조건에서는 부득이하게 생략하였다. 다만, 유량의 정확도는 조건 A의 검증 결과만으로도 충분한 것으로 판단된다.
Fig. 6,7,8을 통해 각 위치에서의 dP와 dQ를 비교해보면 그 값들이 모두 실험과 유사한 것을 확인할 수 있으므로, 두 M&S 방법 모두 실험에서의 유량과 압력 변동을 적절히 모사하고 있음을 알 수 있다.
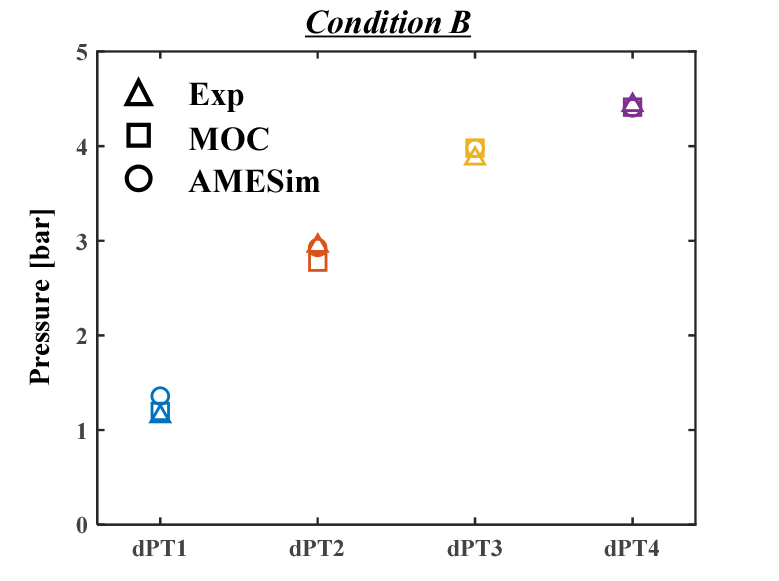
먼저 조건 A의 비교 결과를 보면, Case1과 Case2는 시간에 따른 밸브 개도의 변화가 0.25로 동일하나, 초기 개도율이 다르기 때문에 유량의 변화율에 차이가 있다. Case1의 경우 Case2에 비해 작은 개도에서 시작하므로 초기 유량은 더 작을 수 있으나 NV2의 유량계수 특성상, R이 증가할수록 유량 계수의 증가율이 점차적으로 감소하기 때문에 유량의 변화율은 Case1이 더 크다. 또한 유량 변화의 차이로 인해 압력 변화 역시 두 결과가 상이했다. 한편, 조건 B의 경우, 밸브가 완전히 폐쇄되며 유량이 짧은 시간 동안 크게 변화하기 때문에 유체의 운동에너지가 모두 압력으로 변환된다. 따라서 Fig. 6에 나타난 것과 같이 모든 위치에서의 dP가 이전 조건의 결과 대비 훨씬 더 큰 것을 확인할 수 있다. 특히 구동되는 밸브인 EV와 가장 근접한 위치일수록 그 값이 증가하는 것을 볼 수 있다.
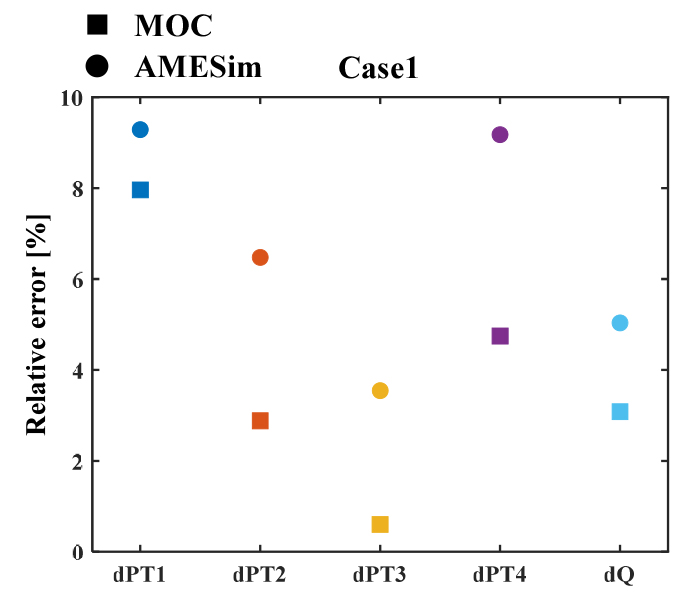
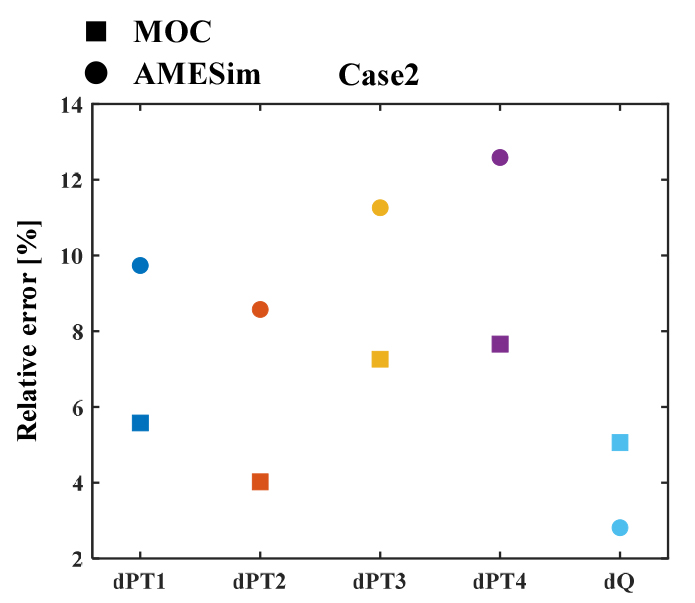
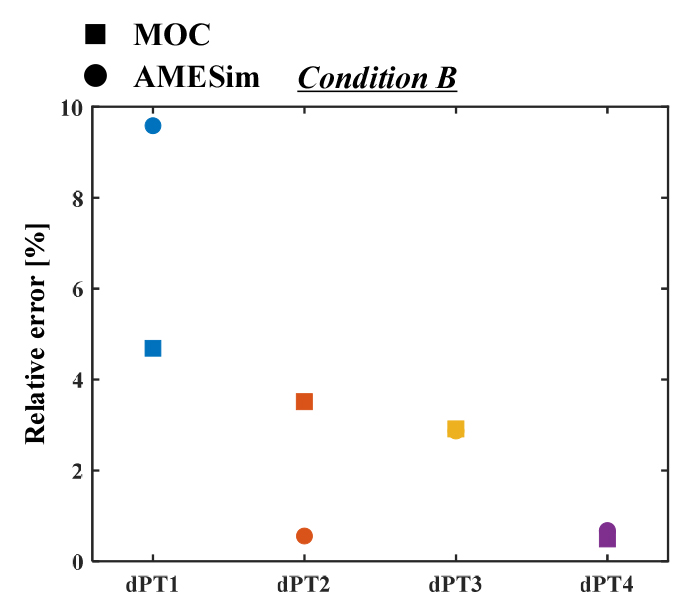
다음으로 Fig. 6,7,8를 바탕으로 특성곡선법 코드와 AMESim의 결과를 실험 대비 상대 오차로 Fig. 9,10,11에 나타내어 정확도를 확인하였다.
유량의 경우, 두 케이스에 대해 약 3% ~ 5%의 오차를 보였으며 압력의 경우, 모든 결과에서 전반적으로 10% 이내였다. 오차의 원인으로는 마찰에 의한 압력 손실 예측의 부정확 때문인 것으로 사료된다. 마찰 손실을 예측하기 위해 파이프의 상대 조도 값을 이용하는데, 이때 시스템의 실제 조도 값을 알기 어려워, 일반적으로 사용하는 조도 값을 활용하였는데, 이로 인해 오차가 발생한 것으로 추측되며 이는 동적 조건에서 더욱 크게 발생된다. 이러한 이유로 일반적으로 실험을 통해 시스템에 맞도록 보정하는 과정을 추가 한다[20]. Fig. 6-7에 제시한 조건 A의 경우, 특성곡선법 코드의 결과가 AMESim에 비해 실험 결과와의 오차가 작으나 조건 B에서는 그 경향이 다르다. 이는 앞서 언급한 바와 같이 조건 B에서는 동적 특성이 강하기 때문인 것으로 추정된다. 실제 두 M&S 기법에서 동적 마찰 계수를 계산하는 방식이 다른데, 과도 층류 구간에 대해 Zielke의 식은 순간 평균 유속과 이전의 유속 변화 가중치를 활용하는데 반해, Brunone의 식은 순간 평균 유속, 국부 가속도, 대류 가속도를 통해 동적 마찰항을 도출한다. Brunone 식의 경우, 식의 구성이 단순하여 사용이 용이하고 마찰 계수를 보정하는 과정을 보다 편리하게 수행할 수 있다는 장점이 있다. 한편, Zielke 식은 상대적으로 낮은 레이놀즈 수의 난류 유동에서 더 높은 정확도를 보인다는 장점이 있으나, 특성곡선법을 활용한 계산에 적용하는 경우 다른 식들에 비해 다소 많은 계산 시간이 소요된다. 하지만 정확도의 감소 없이 계산 효율성을 증가시킬 수 있는 수치적 방안이 적용되어 사용되고 있다[21]. AMESim에서 Zielke 식이 적용되지만 계산 시간이 증가하지 않도록 구현되어[22] 연산량에는 영향을 미치지 않는다.
4.2 계산 소요 시간
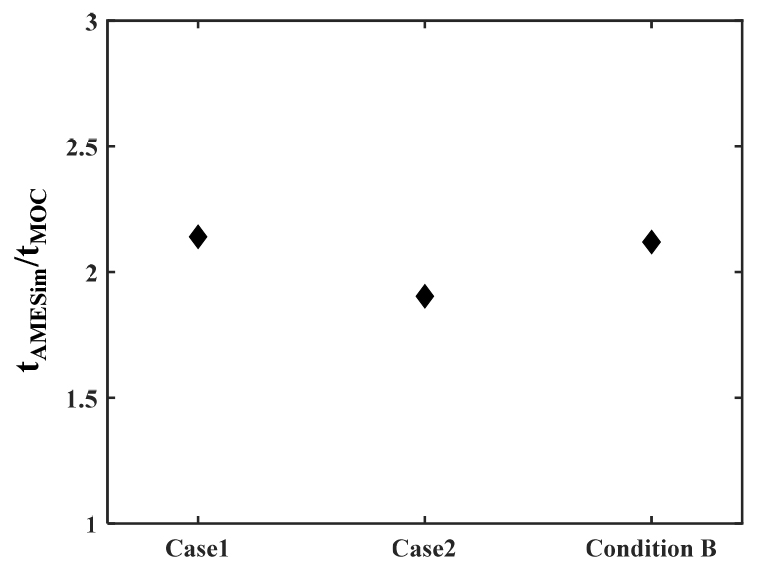
다음으로 특성곡선법 대비 AMESim의 계산 소요 시간을 무차원화하여 Fig. 12에 나타냄으로써 두 M&S 방법의 성능 차이를 비교하였다.
이를 통해 특성곡선법을 통한 M&S가 AMESim M&S 대비 약 2배 정도 짧은 것을 확인할 수 있다. 동일한 조건에서 해석을 수행했음에도 특성곡선법을 적용할 경우에는 편미분 방정식을 상미분 방정식으로 변환하여 결과적으로 연립 방정식을 계산하는 것이나, AMESim의 경우, Lax – Wendroff 방법을 사용하여 full 편미분 방정식인 1D Navier – Stokes 방정식을 계산하는 것이므로 계산 시간에 차이가 발생함을 확인할 수 있다.
5. 결 론
본 연구에서는 특성곡선법을 적용한 코드와 AMESim, 두 가지 M&S 방법으로 액체 추진제를 사용하는 엔진의 공급 과정을 해석하고 이에 대한 결과를 비교하였다. 각각 특성곡선법과 상용프로그램의 Lax – Wendroff 방법을 이용하여 해석하고 실험을 수행하여 그 결과를 바탕으로 두 M&S 방법을 검증하였다. 이를 통해, 밸브, 펌프 등의 여러 부품으로 구성된 시스템에서 비압축성 유체의 정상 및 비정상 상태에 대한 해석이 가능하며, 특히 밸브의 변화에 의한 특성을 예측하는 것에 활용될 수 있음을 확인하였다. 또한 최종적으로는 두 M&S 결과를 실험 대비 상대 오차로 산출하여 정확도를 파악하고 측정한 계산 시간을 비교함으로써 두 성능을 분석하였다. 동적 특성이 경향성에 영향을 미칠 수 있음을 확인하였고 동일한 조건의 해석을 수행함에도 M&S 방법에 따라 성능에 차이가 발생할 수 있다는 것을 볼 수 있다. 결과적으로 전반적인 오차율과 계산 시간을 감안하였을 때, 특성곡선법을 활용한 M&S 방법이 성능 측면에서 좀 더 우수함을 확인하였다.